Next: Bibliography Up: Notes on Landau damping Previous: Two-stream instability
-- -- -- -- As is given in the wikipedia, the ponderomotive force is a
nonlinear force that a charged particle experiences in an inhomogeneous
oscillating electromagnetic field. The ponderomotive force
![]() is
expressed by
is
expressed by
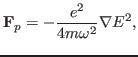 |
(94) |
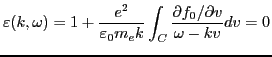
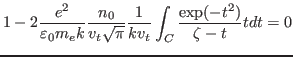
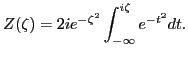 |
(95) |
| (96) |
| (97) |
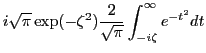 |
|||
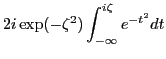 |
(98) |
yj 2016-01-26