Inverse Landau damping

Choose a drift-Maxwellian distribution

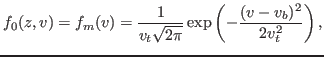$$f_0 (z, v) = f_m (v) = \frac{1}{v_t \sqrt{2 \pi}} \exp \left( - \frac{(v - v_b)^2}{2 v_t^2} \right),$$ (11)

with $v_b / v_p = 2$. Then the derivative of the distribution function with respect to the velocity in the resonant region will be positive. This is the case where an inverse Landau damping is expected to appear.

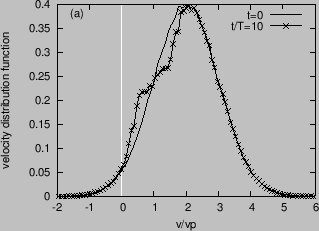
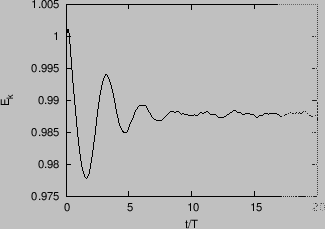
Figure 3 compares the velocity distribution function at $\overline {t} = 0$ and $\overline {t} = 10$, which shows that the distribution is flatted in the resonant region $v / v_p = 1$. Figure 4 plots the temporal evolution of the total kinetic energy of the particles, which confirms that the kinetic energy is reduced by the wave.

Figure 3: Comparison of the velocity distribution function (spatially averaged) at various time, which shows that the distribution is distorted in the resonant region ( $v / v_p \approx 1$). Other parameters: $v_t / v_p = 1$, $2 \pi k q E / m \omega ^2 = 1$.

Figure: Temporal evolution of the total kinetic energy of the particles, where $\overline{E}_k = \sum_{i = 1}^{i = N} \frac{1}{2} m v^2_i / E_{k 0}$, $E_{k 0}$ is the initial total kinetic energy. Other parameters: $v_t / v_p = 1$, $2 \pi k q E / m \omega ^2 = 1$.