Next: misc contents Up: Numerical results for EAST Previous: Local magnetic shear
Next, consider the calculation of matrix elements ![]() . In cylindrical
coordinates, we have
. In cylindrical
coordinates, we have
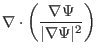 |
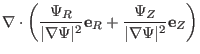 |
||
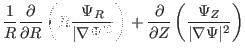 |
|||
![$\displaystyle \frac{\Psi_R}{R \vert \nabla \Psi \vert^2} + \frac{\partial}{\par...
...{\vert \nabla \Psi \vert^4} (2 \Psi_R
\Psi_{R Z} + 2 \Psi_Z \Psi_{Z Z}) \right]$](img851.png) |
|||
![$\displaystyle \frac{\Psi_R}{R \vert \nabla \Psi \vert^2} + \Psi_{R R} \left( \f...
...{\vert \nabla \Psi \vert^4} (2 \Psi_R
\Psi_{R Z} + 2 \Psi_Z \Psi_{Z Z}) \right]$](img852.png) |
|||
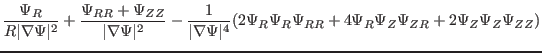 |
(300) |
![]() can also be calculated in the magnetic surface coordinates.
can also be calculated in the magnetic surface coordinates.
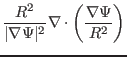 |
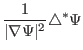 |
||
![$\displaystyle \frac{1}{\vert \nabla \Psi \vert^2} \left[ -{\textmu}_0 R^2 \frac{d p_0}{d
\Psi} - \frac{d g}{d \Psi} g (\Psi) \right] .$](img862.png) |
(304) |
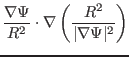 |
![$\displaystyle \frac{\Psi'}{R^2} \left[ \vert \nabla \psi \vert^2
\frac{\partial...
...}{\partial \theta} \left(
\frac{R^2}{\vert \nabla \Psi \vert^2} \right) \right]$](img864.png) |
(305) |
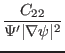 |
![$\displaystyle \Psi' \left[ {\textmu}_0
\frac{d p_0}{d \Psi} \frac{R^2}{\vert \n...
...}{\partial \theta} \left( \frac{R^2}{\vert \nabla \Psi \vert^2}
\right) \right]$](img866.png) |
(306) |
yj 2015-09-04