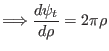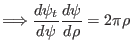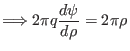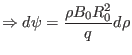We know that the toroidal flux 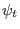 , safety factor
, safety factor 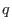 , and the
, and the  in
the GS equation are related by the following equations:
in
the GS equation are related by the following equations:
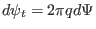 |
(532) |
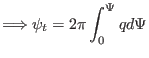 |
(533) |
Define:
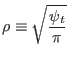 |
(534) |
(In the Toray_ga code, the radial coordinate 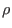 is defined as
is defined as
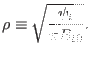 |
(535) |
where 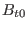 is a constant factor.
is a constant factor.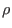 defined this way is of length
dimension, which is an effective geometry radius obtained by approximating the
flux surface as circular.)
defined this way is of length
dimension, which is an effective geometry radius obtained by approximating the
flux surface as circular.)
I use Eq. (534) to define 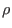 . Then we have
. Then we have
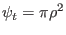 |
(536) |
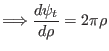 |
(537) |
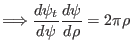 |
(538) |
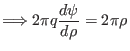 |
(539) |
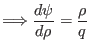 |
(540) |
Eq. (540) is used to transform between 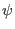 and
and 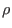 .
.
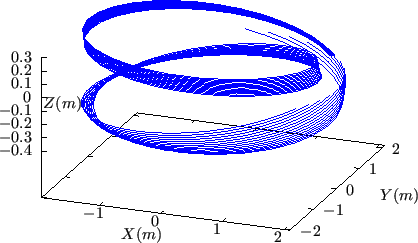
Figure 36:
to be delted, Isosurface of
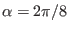 . The surface is
made of a family of contours of
. The surface is
made of a family of contours of
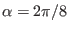 , which are all magnetic
field lines. These field lines are traced by starting from a series of
points on the low-field-side midplane
, which are all magnetic
field lines. These field lines are traced by starting from a series of
points on the low-field-side midplane
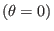 at different radial
locations and the field lines are followed by a complete poloidal loop.
Magnetic field from EAST discharge #59954@3.03s.
at different radial
locations and the field lines are followed by a complete poloidal loop.
Magnetic field from EAST discharge #59954@3.03s.
 |
yj
2018-03-09
![]() , safety factor
, safety factor ![]() , and the
, and the ![]() in
the GS equation are related by the following equations:
in
the GS equation are related by the following equations:
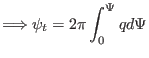
![]() . Then we have
. Then we have