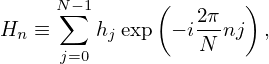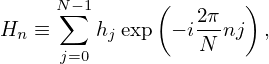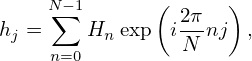5 About using the FFT library
FFTW/scipy uses negative exponents as the forward transform and and the positive
exponents as inverse transform. Specifically, the forward DFT in FFTW is defined
by
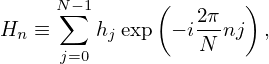 | (53) |
and the inverse DFT is defined by
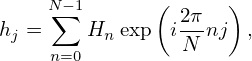 | (54) |
where there is no 1∕N factor in the inverse DFT, and thus this factor should be
included manually if we want to recover the original data from the inverse DFT. (In
some rare cases, e.g. in the book “Numerical recipe”[2], positive exponents are used
in defining the forward Fourier transformation and negative exponents are used in
defining the backward one. When using a Fourier transformation library, it is
necessary to know which convention is used in order to correctly use the output of
the library.)
In Scipy:
def fft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None, *,
plan=None):
#norm : {"backward", "ortho", "forward"}, optional
Normalization mode. Default is "backward", meaning no normalization on
the forward transforms and scaling by 1/n on the ifft.
"forward" instead applies the 1/n factor on the forward tranform.
For norm="ortho", both directions are scaled by 1/sqrt(n).
I use the Fortran interface of the FFTW library. To have access to FFTW library, use
the following codes:
use, intrinsic :: iso_c_binding
implicit none
include ’fftw3.f03’
Here the first line uses iso_c_binding module to interface with C in which FFTW is
written. To use the FFT subroutines in FFTW, we need to define some variables of
the desired types, such as
type(C_PTR) :: plan1, plan2
complex(C_DOUBLE_COMPLEX) :: in(0:n-1), out(0:n-1)
Specify what kind of transform to be performed by calling the corresponding
“planner” routine:
plan1 = fftw_plan_dft_1d(n, in,out, FFTW_FORWARD,FFTW_ESTIMATE)
Here the “planner” routine for one-dimensional DFT is called. One thing that the
“planner” routine does is to factor the matrix Mkj mentioned above, in order to
get prepared for performing the actual transform. Therefore “planner” do
not need the actual data stored in “in” array. What is needed is the length
and numerical type of “in” array. It is obvious that the “planner” routine
needs to be invoked for only once for a given type of array with the same
length.
Store input data in the “in” arrays, then, we can perform a DFT by the following
codes:
call fftw_execute_dft(plan1, in, out)
Similarly, we can perform a inverse DFT by the following codes:
plan2 = fftw_plan_dft_1d(ngrids, in,out,FFTW_BACKWARD,FFTW_ESTIMATE)
call fftw_execute_dft(plan2, in, out)
After all the transforms are done, we need to manually de-allocate the arrays
created by the “planner” routine by calling the “fftw_destroy_plan” routine:
call fftw_destroy_plan(plan2)
(Unless they are local arrays, Fortran does not automatically de-allocate arrays
allocated by the acllocate(), so manually de-allocate all allocated arrays is
necessary for avoid memory leak)