[tail] [up]

D.1 Computing Fourier integrals using FFT (not finished, to be deleted)

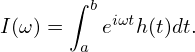
Consider the calculation of the following integral:

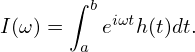∫ b I(ω ) = eiωth(t)dt. a
(141)

Divide the interval [a,b] into M uniform sub-intervals and define

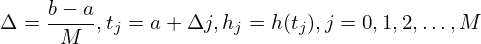b− a Δ = ----,tj = a + Δj,hj = h(tj),j = 0,1,2,...,M M
(142)

Then the integration in Eq. (141) can be approximated as

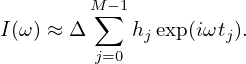M∑−1 I(ω) ≈ Δ hj exp (iωtj). j=0
(143)

Define ωm = 2πm∕(MΔ) with integer m and −M∕2 < m < M∕2. Consider the calculation of I(ωm). Using Eq. (143), we obtain

M∑ −1 I(ωm) = Δ hjexp[iωm (a+ Δj)] j=0 M−1 = Δeiωma ∑ hjexp(iωm Δj) j=0 M−1 ( ) = Δeiωma ∑ hjexp i2πm-j j=0 M iωma = Δe iω aHm (144) = Δe m [DFT (h0,h1,h2,...,hM −1)]m. (145)
Equation (145) indicates the value of the integration I(ωm) can be obtained by calculating the discrete Fourier transformation of hj. However, as discussed in Ref. [2], equation (145) is not recommended for practical use because the oscillatory nature of the integral will make Eq. (145) become systematically inaccurate as ω increases. Next, consider a new method, in which h(t) is expanded as
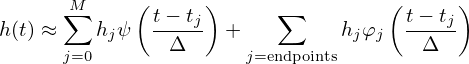M∑ ( t− tj) ∑ ( t− tj) h(t) ≈ hjψ --Δ-- + hjφj --Δ-- j=0 j=endpoints
(146)

Apply the integral operator∫ abdtexp(iωt) to both sides of Eq. (146), we obtain

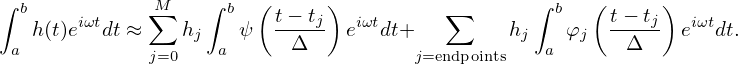∫ b ∑M ∫ b ( ) ∑ ∫ b ( ) h(t)eiωtdt ≈ hj ψ t−-tj eiωtdt+ hj φj t-− tj eiωtdt. a j=0 a Δ j=endpoints a Δ
(147)

Make the change of variables s = (t−tj)∕Δ in the first integral and s = (t−a)∕Δ in the second integral, the above equation is written as

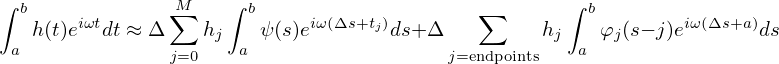∫ b ∑M ∫ b ∑ ∫ b h(t)eiωtdt ≈ Δ hj ψ(s)eiω(Δs+tj)ds+ Δ hj φj (s− j)eiω(Δs+a)ds a j=0 a j=endpoints a
(148)

Define 𝜃 = ωΔ and make use of tj = a + jΔ, the above equation is written as

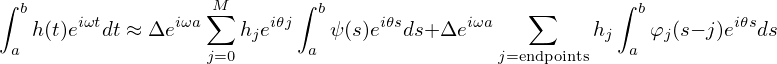∫ ∫ ∫ b iωt iωa M∑ i𝜃j b i𝜃s iωa ∑ b i𝜃s a h(t)e dt ≈ Δe hje a ψ(s)e ds+ Δe hj a φj(s− j)e ds j=0 j=endpoints
(149)

Define

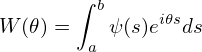∫ b W (𝜃) = ψ (s)ei𝜃sds a
(150)

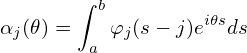∫ b i𝜃s αj(𝜃) = a φj(s− j)e ds
(151)

Then Eq. (149) is written as

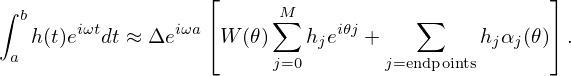⌊ ⌋ ∫ b ∑M ∑ h (t)eiωtdt ≈ Δeiωa⌈W (𝜃) hjei𝜃j + hjαj(𝜃)⌉. a j=0 j=endpoints
(152)

 

 

 

 

 

pict

Figure 8: Older version of Fig. ??, created by Metapost, the new version is created by the vector graphic editor in TeXmacs.

 

[front] [up]