5.9 Width of guiding center orbit

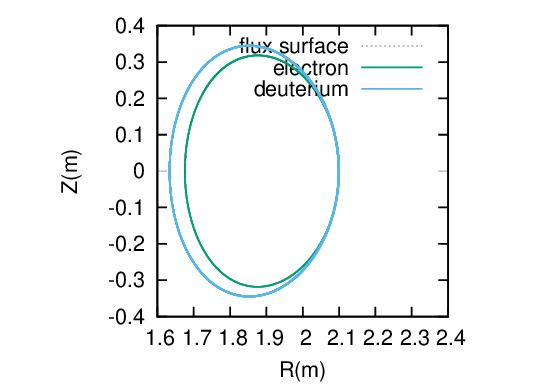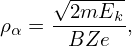
The gyroradius of a particle is given by ρ_α = mv∕BZe, which can be further written as

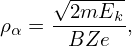(104)

where E_k is the kinetic energy of the particle. For an electron with the same kinetic energy of a ion, Eq. (104) indicates that the gyroradius of the electron is smaller than that of the ion by the factor 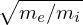. Now comes the question: Is the width of the guiding center orbit of an electron with the same kinetic energy of a ion smaller than that of the ion? Examine the constant of motion P_ϕ which is given by

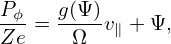(105)

The function g(Ψ)∕Ω is usually a weak function of Ψ, thus can be asssumed to be a contant along a drift orbit. The orbit width can be characterised by ΔΨ, which is written

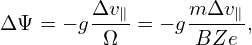(106)

where Δv_∥ is the variation range of v_∥ in one poloidal period of the orbit. For trapped particles, this variation can be approximated as

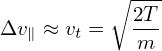(107)

Using this, Eq. (106) is written as

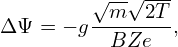(108)

which indecates that, for the same temperature, ΔΨ is proportional to 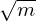. (For circulationg ions, the variation of v_∥ during one poloidal period can not be approximated by v_t. I do not know how to estimate the orbit width in this case).

The variation of the poloidal flux ΔΨ_p can be approximated by

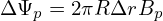(109)

where Δr is the variation of the minor radius, B_p is the average poloidal magnetic field on a magnetic surface. Using this and the defintion ΔΨ = ΔΨ_p∕2π in Eq. (108), we obtain

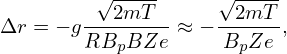(110)

which indicates that the width of guiding-center orbits is inversely proportional to the poloidal magnetic field B_p, rather than the toroidal magnetic field B_t (first got to know this conclusion from J. Wession’s book “Science of JET”, and later wrote the above derivation).

Comparing Eq. (110) and (104), we know Δr is just the “poloidal larmor radius” which is obtained by replacing the B in Eq. 104) by the poloidal magnetic field B_p. It follows that the ratio between them is given by

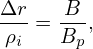(111)

which is about q∕𝜀 for large aspect-ratio tokamaks, where q is the safety factor.

The average poloidal magnetic field on a magnetic surface neare the plasma edge is approximately given by

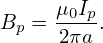(112)

Using this, Eq. (110) is written as

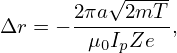(113)

which indicates that Δr is proportional to 1∕I_p. This explains why high plasma current is beneficial to the confinement of energetic particles (because high current corresponds to smaller orbit width and thus better confinement of energetic particles which usually have larger drift orbit width than thermal particles).

A numerical example in Fig. 25 indicate, as expected, that the guiding center orbit width of an electron with the same kinetic energy of a ion is much smaller than that of the ion.