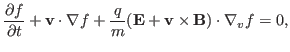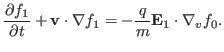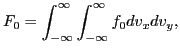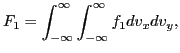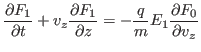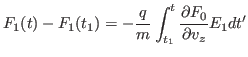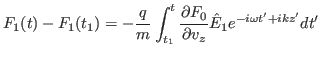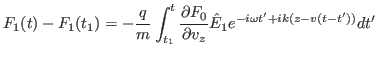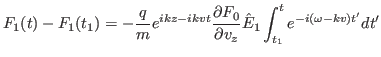In this section, we consider the self-consistent-field theory of Landau
damping. The Vlasov equation is written
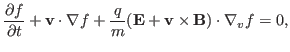 |
(58) |
where 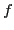 is the electron distribution function,
is the electron distribution function, 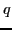 and
and 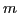 are the charge
and mass of electrons, respectively. The linearized version of the above
equation is written
are the charge
and mass of electrons, respectively. The linearized version of the above
equation is written
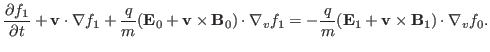 |
(59) |
We consider the case of
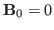 and
and
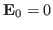 . Further
consider only the electrostatic case, i.e.
. Further
consider only the electrostatic case, i.e.
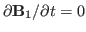 , i.e., there is not magnetic fluctuation. Then it follows from Faraday's
law that the perturbed electric field can be written as
, i.e., there is not magnetic fluctuation. Then it follows from Faraday's
law that the perturbed electric field can be written as
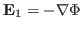 . Then the linearized Vlasov equation (59) is written
. Then the linearized Vlasov equation (59) is written
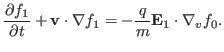 |
(60) |
Consider the one-dimensional case where 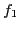 , and
, and 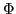 are both independent
of
are both independent
of 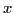 and
and 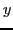 coordinates, then the above equation is written
coordinates, then the above equation is written
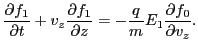 |
(61) |
Integrating both sides of Eq. (61) over 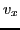 and
and 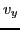 , we obtain
, we obtain
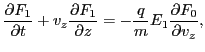 |
(62) |
where
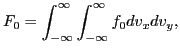 |
(63) |
and
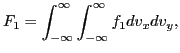 |
(64) |
which are called the reduced distribution functions. Poisson's equation is
written
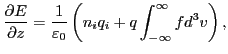 |
(65) |
where 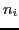 and
and 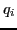 are the number density and charge of ions, respectively.
In equilibrium the number density of electrons and ions are equal to each
other. Assuming the number density of the massive ions remain unchanged,
Poisson's equation for the perturbed quantities is written
are the number density and charge of ions, respectively.
In equilibrium the number density of electrons and ions are equal to each
other. Assuming the number density of the massive ions remain unchanged,
Poisson's equation for the perturbed quantities is written
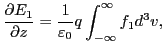 |
(66) |
In terms of the reduced distribution function, equation (66) is
written
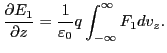 |
(67) |
Equations (62) and (67) governs the time evolution of
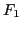 and
and 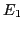 . Consider the case that
. Consider the case that 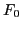 is spatially uniform, then all
the coefficients of Eqs. (62) and (67) are independent of
the spatial coordinate. In this case, different spatial Fourier harmonics are
decoupled. Therefore, we can consider the case that there are only one Fourier
harmonics
is spatially uniform, then all
the coefficients of Eqs. (62) and (67) are independent of
the spatial coordinate. In this case, different spatial Fourier harmonics are
decoupled. Therefore, we can consider the case that there are only one Fourier
harmonics 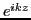 in both
in both 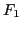 and
and 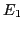 , i.e.,
, i.e., 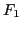 and
and 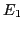 are
written, respectively, as
are
written, respectively, as
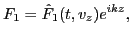 |
(68) |
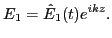 |
(69) |
Note that 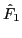 and
and 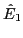 in Eqs (68) and
(69) are usually complex-valued (to allow arbitrary phases angle in
in Eqs (68) and
(69) are usually complex-valued (to allow arbitrary phases angle in
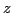 ). Then using Eq. (67) in Eq. (62) yields
). Then using Eq. (67) in Eq. (62) yields
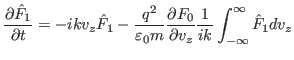 |
(70) |
Given an equilibrium distribution function 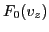 and an initial
perturbation
and an initial
perturbation
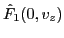 , equation (70) can be solved
analytically by using the Laplace transformation. Here, to avoid the fancy
mathematics involved in the Laplace transformation, I solve Eq.
(70) by a direct numerical method.
, equation (70) can be solved
analytically by using the Laplace transformation. Here, to avoid the fancy
mathematics involved in the Laplace transformation, I solve Eq.
(70) by a direct numerical method.
-- -- tmp
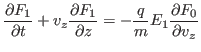 |
(71) |
Using
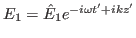 , the above equation is
written
, the above equation is
written
-- -- tmp
yj
2016-01-26