Next: Phase mixing and linear Up: Self-consistent-field simulation of linear Previous: One-dimensional Vlasov-Poisson equations
The reduced equilibrium distribution function ![]() satisfies the
normalization condition
satisfies the
normalization condition
![]() ,
where
,
where ![]() the number density of electrons. Denote the thermal velocity of
the equilibrium distribution by
the number density of electrons. Denote the thermal velocity of
the equilibrium distribution by ![]() . Then Eq. (70) can be written
. Then Eq. (70) can be written
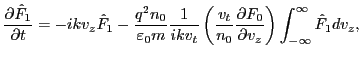 |
(72) |
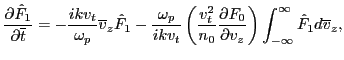 |
(74) |