Next, we compare the numerical results with the electron plasma wave
dispersion relation, which is given by[1]
![$\displaystyle 1 + 2 \left( \frac{\omega_p}{k v_t} \right)^2 [1 + \zeta Z (\zeta)] = 0,$](img267.png) |
(83) |
where
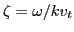 , and
, and
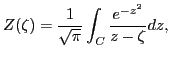 |
(84) |
is the plasma dispersion function. The plasma dispersion function is related
to the error function of imaginary argument by
 |
(85) |
The
 function is implemented in Wolfram Mathematica. By using
function is implemented in Wolfram Mathematica. By using
 function of Wolfram Mathematica, the equation (83)
can be easily solved numerically to find the root. For the parameter used in
the simulation
function of Wolfram Mathematica, the equation (83)
can be easily solved numerically to find the root. For the parameter used in
the simulation
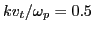 ,
,
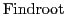 gives
gives
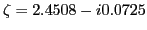 . From this, we obtain
. From this, we obtain
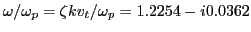 .
.
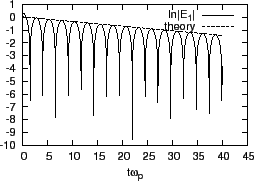
The oscillation frequency of the electric field can be estimated by counting
the peaks in Fig. 8, from which we obtain
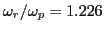 , which agrees the theoretic value
, which agrees the theoretic value 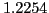 given above. Figure
8 shows that the amplitude of the electric filed decreases
exponentially with time. Figure 9 compares the theoretic growth rate
with the simulation results, which also shows good agreement with each other.
given above. Figure
8 shows that the amplitude of the electric filed decreases
exponentially with time. Figure 9 compares the theoretic growth rate
with the simulation results, which also shows good agreement with each other.
Figure 9:
Comparison of the damping rate given by Eq.
(83)
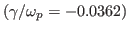 with the simulation results.
with the simulation results.
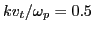 .
.
 |
In the weak growth rate approximation, the real frequency of electron plasma
wave is given by
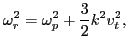 |
(86) |
for a Maxwellian plasma. For the numerical case given here,
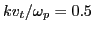 . Using this in Eq. (86), we obtain
. Using this in Eq. (86), we obtain
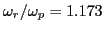 , which roughly agrees with the exact value
, which roughly agrees with the exact value
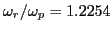 .
.
In the weak growth rate approximation, the growth rate is given by Eq.
(45), i.e.,
![$\displaystyle \gamma = \frac{\pi \omega \omega_p^2}{2\vert k\vert k} \frac{1}{n_0} \left[ \frac{d f_0 (v)}{d v} \right]_{v = \omega / k},$](img282.png) |
(87) |
Using this, we obtain
From this, we obtain
![$\displaystyle \frac{\gamma}{\omega_p} = \sqrt{\pi} \frac{\omega_p}{k v_t} \left...
...\left( - \frac{\omega^2 / \omega_p^2}{k^2 v_t^2 / \omega_p^2} \right) \right] .$](img286.png) |
(89) |
Using
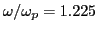 in Eq. (89), we obtain
in Eq. (89), we obtain
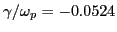 , which roughly agrees with the exact value
, which roughly agrees with the exact value
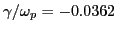 obtained above. Note that if we used
obtained above. Note that if we used
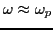 , instead of the exact frequency
, instead of the exact frequency
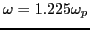 , then Eq.
(89) would give
, then Eq.
(89) would give
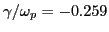 , which is almost one
order larger than the exact value
, which is almost one
order larger than the exact value
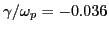 . This
highlights the inaccuracy of the approximate formula we encounter in
textbooks[1], where
. This
highlights the inaccuracy of the approximate formula we encounter in
textbooks[1], where
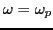 is used to estimate
the damping rate.
is used to estimate
the damping rate.
yj
2016-01-26
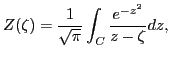
![]() , which agrees the theoretic value
, which agrees the theoretic value ![]() given above. Figure
8 shows that the amplitude of the electric filed decreases
exponentially with time. Figure 9 compares the theoretic growth rate
with the simulation results, which also shows good agreement with each other.
given above. Figure
8 shows that the amplitude of the electric filed decreases
exponentially with time. Figure 9 compares the theoretic growth rate
with the simulation results, which also shows good agreement with each other.
![$\displaystyle \gamma = \frac{\pi \omega \omega_p^2}{2\vert k\vert k} \frac{1}{n_0} \left[ \frac{d f_0 (v)}{d v} \right]_{v = \omega / k},$](img282.png)