Next: Two-stream instability Up: Self-consistent-field simulation of linear Previous: Comparison with linear theory
In the above, we see that the integration
![]() decreases with time, which seems to be inconsistent with
the conservation of particle number. Note the spatial dependence of the
perturbed distribution function is
decreases with time, which seems to be inconsistent with
the conservation of particle number. Note the spatial dependence of the
perturbed distribution function is ![]() , i.e., the perturbed
distribution function is given by
, i.e., the perturbed
distribution function is given by
![]() , the real part of
which corresponds to the physical distribution function, i.e.,
, the real part of
which corresponds to the physical distribution function, i.e.,
![]() , where
, where
![]() and
and ![]() is
the angle of
is
the angle of ![]() on the complex plane. The particle number for the
distribution function
on the complex plane. The particle number for the
distribution function ![]() in a region of the wave length
in a region of the wave length ![]() is
given by
is
given by
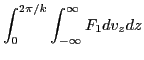 |
|||
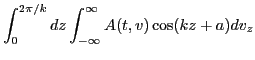 |
|||
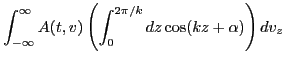 |
(90) |
yj 2016-01-26