Consider the motion of a test particle moving in a longitudinal wave,
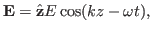 |
(12) |
then the equation of motion is given by
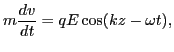 |
(13) |
and
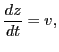 |
(14) |
with initial condition
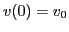 and
and
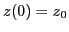 , where
, where
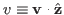 and
and
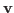 is the velocity of the
particle. Equations (13) and (14) are nonlinear
system, for which exact solutions are hard to be found. Here, we consider the
amplitude of the electrical field,
is the velocity of the
particle. Equations (13) and (14) are nonlinear
system, for which exact solutions are hard to be found. Here, we consider the
amplitude of the electrical field, 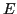 , as a small perturbation, and use the
iterative method[2] to solve Eqs. (13) and
(14) approximately. The initial guess of the solution is obtained
by setting
, as a small perturbation, and use the
iterative method[2] to solve Eqs. (13) and
(14) approximately. The initial guess of the solution is obtained
by setting 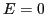 , which gives
, which gives
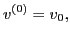 |
(15) |
and
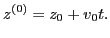 |
(16) |
Substituting this solution back into the right-hand side of Eq.
(13), we obtain
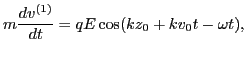 |
(17) |
which can be integrated over time to give
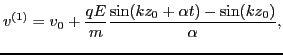 |
(18) |
where
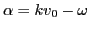 and use has been made of the initial condition
and use has been made of the initial condition
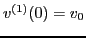 . Substituting this solution for the velocity, Eq.
(14) is written
. Substituting this solution for the velocity, Eq.
(14) is written
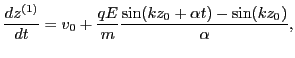 |
(19) |
which can be integrated over time, giving
where use has been made of the initial condition
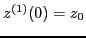 .
Substituting the solution in Eq. (20) back into the right-hand side
of Eq. (13), we obtain
.
Substituting the solution in Eq. (20) back into the right-hand side
of Eq. (13), we obtain
Since  is considered to be a small parameter, the term proportional to
is considered to be a small parameter, the term proportional to  can be considered to be small when compared with
can be considered to be small when compared with
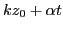 .
Therefore, we expand the first cosine function in the vicinity of
.
Therefore, we expand the first cosine function in the vicinity of
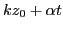 . Thus the above equation is written approximately as
. Thus the above equation is written approximately as
![$\displaystyle m \frac{d v^{(2)}}{d t} \approx q E \cos (k z_0 + \alpha t) - \si...
...+ \alpha t) + \cos (k z_0)}{\alpha^2} - \frac{\sin (k z_0)}{\alpha} t \right] .$](img93.png) |
(22) |
Next, calculate the time change rate of the kinetic energy of the particle,
which is written as
Using Eq. (18) for 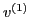 and Eq. (22) for
and Eq. (22) for
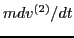 , Eq. (23) is written
, Eq. (23) is written
where the terms of order 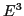 have been neglected (if terms of order
have been neglected (if terms of order 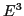 and higher are included, then the result will correspond to nonlinear Landau
damping, is this correct?). Equations (24) agrees with Eq. (8) in
Chapter 8 of Stix's book[4] (however Stix's formula misses, by
mistakes, the first term of the above equation).
and higher are included, then the result will correspond to nonlinear Landau
damping, is this correct?). Equations (24) agrees with Eq. (8) in
Chapter 8 of Stix's book[4] (however Stix's formula misses, by
mistakes, the first term of the above equation).
yj
2016-01-26
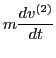
![$\displaystyle q E \cos \left\{ k z_0 + k v_0 t + k \frac{q E}{m} \left[ \frac{-...
... (k z_0)}{\alpha^2} - \frac{t \sin (k
z_0)}{\alpha} \right] - \omega t \right\}$](img90.png)
![$\displaystyle q E \cos \left\{ k z_0 + \alpha t + k \frac{q E}{m} \left[ \frac{...
...t) + \cos (k z_0)}{\alpha^2} - \frac{\sin (k
z_0)}{\alpha} t \right] \right\} .$](img91.png)