Since there is a
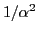 factor in the integrand of the above integral,
the important contribution to the integral must come from the vicinity of
factor in the integrand of the above integral,
the important contribution to the integral must come from the vicinity of
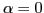 (i.e. resonant particles). Therefore we expand
(i.e. resonant particles). Therefore we expand
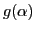 as
as
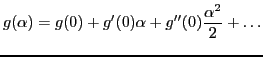 |
(37) |
Since
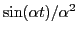 is odd in
is odd in 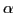 , only terms that are
also odd need to be retained in the above expansion. Using these, expression
(36) is written as
, only terms that are
also odd need to be retained in the above expansion. Using these, expression
(36) is written as
Using these results, Eq. (35) is written as
![$\displaystyle \left\langle \left\langle \frac{d}{d t} \left( \frac{1}{2} m v^2 ...
...\frac{(q E)^2}{2 m} \left[ \frac{d f (v_0)}{d v_0} \right]_{v_0 = \omega / k} .$](img152.png) |
(39) |
which agrees with Eq. (16) in Chapter 8 of Stix's book[4].
Equation (39) indicates that the time rate of change of the
averaged kinetic energy of resonant particles is proportional to the
derivative of the initial distribution function at the phase
velocity of the wave.
yj
2016-01-26
![]() factor in the integrand of the above integral,
the important contribution to the integral must come from the vicinity of
factor in the integrand of the above integral,
the important contribution to the integral must come from the vicinity of
![]() (i.e. resonant particles). Therefore we expand
(i.e. resonant particles). Therefore we expand
![]() as
as
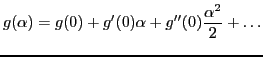
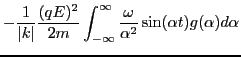
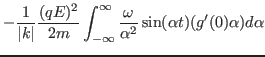
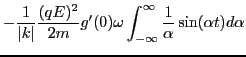
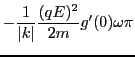
![$\displaystyle - \frac{\pi \omega}{\vert k\vert k} \frac{(q E)^2}{2 m} \left[ \frac{d f
(v_0)}{d v_0} \right]_{v_0 = \omega / k} .$](img151.png)