Examining the expression (138) for matrix element 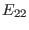 , we find
that the first term of
, we find
that the first term of 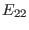 can be written as
can be written as
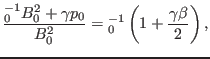 |
(214) |
where
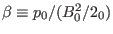 , while the second term of
, while the second term of
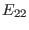 can be written as
can be written as
where
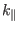 is the parallel wave vector and we have used the
approximation
is the parallel wave vector and we have used the
approximation
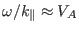 . Using Eqs. (214)
and (215), the ratio of the second term to the first term of
. Using Eqs. (214)
and (215), the ratio of the second term to the first term of
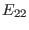 is written as
is written as
![$ (\gamma \beta / 2) / [1 + \gamma \beta / 2]$](img548.png) . For low
. For low
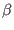 (
(
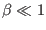 ) equilibrium, the ratio is small and therefore the
second term of
) equilibrium, the ratio is small and therefore the
second term of 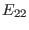 can be dropped. This approximation is called the slow
sound approximation in the literature[6,7]. Numerical
results indicate this approximation will remove all the sound continua while
keeping the Alfven continua nearly unchanged.
can be dropped. This approximation is called the slow
sound approximation in the literature[6,7]. Numerical
results indicate this approximation will remove all the sound continua while
keeping the Alfven continua nearly unchanged.
yj
2015-09-04
![]() , we find
that the first term of
, we find
that the first term of ![]() can be written as
can be written as