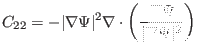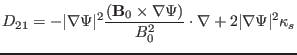Using Eqs. (121) and (122) to eliminate 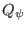 ,
,
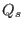 , Eqs. (124) and (125) are written, respectively,
as
, Eqs. (124) and (125) are written, respectively,
as
and
Following Ref. [3], we will express the final eigenmodes
equations in terms of the following four variables: 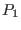 ,
,
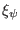 ,
,
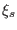 , and
, and
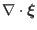 . In order to achieve this, we need
to eliminate unwanted variables. Since we will use
. In order to achieve this, we need
to eliminate unwanted variables. Since we will use
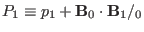 instead of
instead of 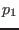 as one of the
variables. we write the equation (120) for the perturbed pressure
in terms of
as one of the
variables. we write the equation (120) for the perturbed pressure
in terms of 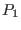 variable, which gives
variable, which gives
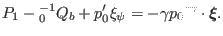 |
(129) |
Using (129) to eliminate 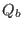 in Eq. (128), we obtain
in Eq. (128), we obtain
Using pressure equation (120) to eliminate 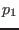 in Eq.
(126), we obtain
in Eq.
(126), we obtain
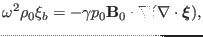 |
(131) |
which can be used in Eq. (123) to eliminate 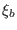 , yielding
, yielding
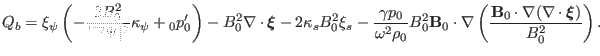 |
(132) |
Using Eq. (132) to eliminate 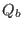 in Eq. (129), we obtain
in Eq. (129), we obtain
![$\displaystyle P_1 +{\textmu}_0^{- 1} \left[ \frac{2 B^2_0}{\vert \nabla \Psi \v...
...^2_0} \right) \right] = - \gamma p_0 \nabla \cdot \ensuremath{\boldsymbol{\xi}}$](img350.png) |
(133) |
Equations (130) and (133), which involves only surface
derivative operators, can be put in the following matrix form:
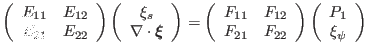 |
(134) |
with the matrix elements given by
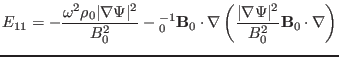 |
(135) |
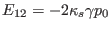 |
(136) |
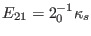 |
(137) |
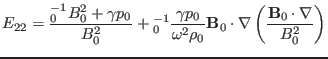 |
(138) |
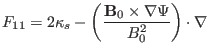 |
(139) |
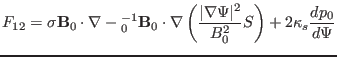 |
(140) |
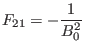 |
(141) |
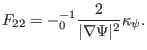 |
(142) |
Equations (134)-(142) agree with equations (25), (28), and
(29) of Ref [3].
Using Eq. (129) to eliminate 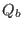 in Eq. (127), we obtain
in Eq. (127), we obtain
The equation for the divergence of
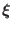 [Eq. (95)] is
written
[Eq. (95)] is
written
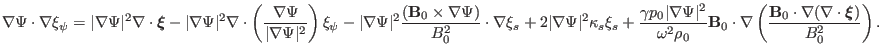 |
(144) |
Equations (143) and (144) can be put in the following
matrix form
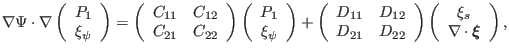 |
(145) |
with the matrix elements given by
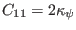 |
(146) |
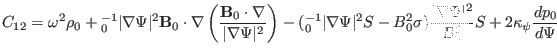 |
(147) |
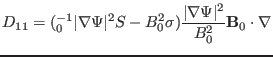 |
(148) |
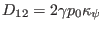 |
(149) |
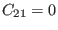 |
(150) |
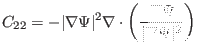 |
(151) |
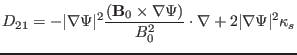 |
(152) |
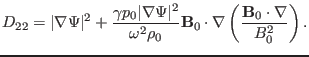 |
(153) |
Equations (146)-(153) agree with Equations (26) and (27)
in Ref.[3]. (It took me several months to manage to put the
equations in the matrix form given here.)
yj
2015-09-04
![]() ,
,
![]() , Eqs. (124) and (125) are written, respectively,
as
, Eqs. (124) and (125) are written, respectively,
as
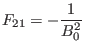
![]() in Eq. (127), we obtain
in Eq. (127), we obtain