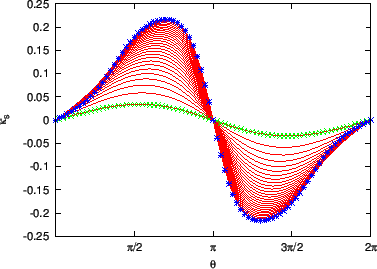
Next, consider the calculation of the surface component of
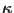 , the geodesic curvature
, the geodesic curvature 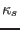 , which is defined by
, which is defined by
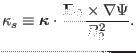 |
(268) |
Using
and Eq. (263), we obtain
Using Eqs. (270), (271), and (272), equation
(268) is written as
The terms in the first line of Eq. (273) is written as
| |
|
![$\displaystyle \frac{g \Psi'^3}{B_0^3} \mathcal{J}^{- 2} \left[
\frac{\partial}{...
...{\theta}^2 + \frac{\mathcal{J}^{- 1}}{B_0} R_{\theta
\theta} R_{\theta} \right]$](img774.png) |
|
| |
|
![$\displaystyle = \frac{g \Psi'^3}{B_0^3} \mathcal{J}^{- 2} \left[
\frac{\partial...
... 1}}{B_0}
(Z_{\theta \theta} Z_{\theta} + R_{\theta \theta} R_{\theta}) \right]$](img775.png) |
(274) |
Noting that
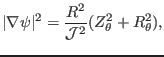 |
(275) |
and
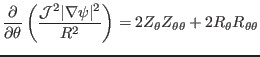 |
(276) |
expression (274) is written as
| |
|
![$\displaystyle \frac{g \Psi'^3}{B_0^3} \mathcal{J}^{- 2} \left[
\frac{\partial}{...
...eta} \left(
\frac{\mathcal{J}^2 \vert \nabla \psi \vert^2}{R^2} \right) \right]$](img778.png) |
|
| |
|
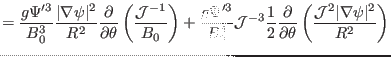 |
(277) |
The first two terms on the second line of Eq. (273) can be written
as
![$\displaystyle - \frac{g \Psi'^3}{B_0^3} \vert \nabla \psi \vert^2 \mathcal{J}^{...
...eft( \frac{1}{R B_0} \right) \frac{1}{R} + \frac{1}{B_0 R^3} R_{\theta} \right]$](img780.png) |
(278) |
The sum of the expression (278) and the first term of expression
(277) is written as
Using the above results, 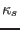 is written as
is written as
Using
equation (281) is written
Excluding the
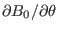 term, the other terms on the
r.h.s of the above equation are written
term, the other terms on the
r.h.s of the above equation are written
Therefore equation (8.4.2) is written
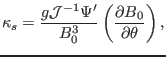 |
(282) |
which agrees with the formula given in Ref. [6]. Equation
(282) takes a very simple form, and provides a clear physical
meaning for the geodesic curvature: 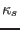 is proportional to the poloidal
derivative of the magnetic field strength. Equation (
is proportional to the poloidal
derivative of the magnetic field strength. Equation (![[*]](crossref.png) ) indicates
that the geodesic curvature is zero for an equilibrium configuration that is
uniform in poloidal direction. Note that this formula for
) indicates
that the geodesic curvature is zero for an equilibrium configuration that is
uniform in poloidal direction. Note that this formula for 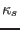 is valid
for arbitrary Jacobian. (Remarks: When I derived the formula of
is valid
for arbitrary Jacobian. (Remarks: When I derived the formula of 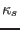 for
the first time, I found that
for
the first time, I found that 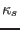 can be written in the simple form
given by Eq. (282) for the equa-arc length Jacobian. Later I found
that
can be written in the simple form
given by Eq. (282) for the equa-arc length Jacobian. Later I found
that 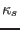 can also be written in the simple form given by Eq.
(282) for the Boozer Jacobian. This makes me realize that the simple
form given by Eq. (282) may be universally valid for arbitrary
Jacobian. However, I did not verify this then. About two years later, I
reviewed this notes and succeeded in providing the derivation given above. The
derivation given above seems to be tedious and may be greatly simplified in
some aspects. But, at present, the above derivation is the only one that I can
provide.)
can also be written in the simple form given by Eq.
(282) for the Boozer Jacobian. This makes me realize that the simple
form given by Eq. (282) may be universally valid for arbitrary
Jacobian. However, I did not verify this then. About two years later, I
reviewed this notes and succeeded in providing the derivation given above. The
derivation given above seems to be tedious and may be greatly simplified in
some aspects. But, at present, the above derivation is the only one that I can
provide.)
If we choose the equal-arc Jacobian, then Eq. (280) becomes
relatively simple:
![$\displaystyle \kappa_s = \frac{g \Psi'^3}{B_0^4} \frac{1}{\mathcal{J}^2} \left[...
...{J}^{- 1}) \right] - \frac{\Psi' g^3}{R^3 B_0^4} \mathcal{J}^{- 1} R_{\theta} .$](img802.png) |
(283) |
This form is implemented in GTAW code. Figure 31 gives the results
for 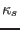 calculated by using Eq. (283). I have verified
numerically that the results given by Eqs. (282) and (283)
agree with each other.
calculated by using Eq. (283). I have verified
numerically that the results given by Eqs. (282) and (283)
agree with each other.
Figure 31:
The geodesic magnetic curvature 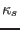 (calculated by Eq. (283)) as a function of the poloidal angle. The
different lines corresponds to different magnetic surfaces. The stars
correspond to the values of
(calculated by Eq. (283)) as a function of the poloidal angle. The
different lines corresponds to different magnetic surfaces. The stars
correspond to the values of 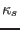 on the boundary magnetic surface
while the plus signs correspond to the value on the innermost magnetic
surface (the magnetic surface adjacent to the magnetic axis). The
equilibrium is a Solovev equilibrium.
on the boundary magnetic surface
while the plus signs correspond to the value on the innermost magnetic
surface (the magnetic surface adjacent to the magnetic axis). The
equilibrium is a Solovev equilibrium.
 |
yj
2015-09-04
![]() , the geodesic curvature
, the geodesic curvature ![]() , which is defined by
, which is defined by
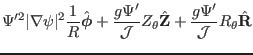
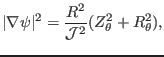
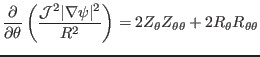
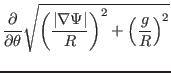
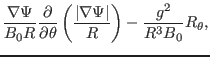
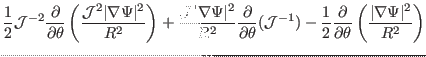
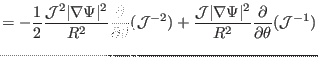
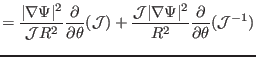
![[*]](crossref.png) ) indicates
that the geodesic curvature is zero for an equilibrium configuration that is
uniform in poloidal direction. Note that this formula for
) indicates
that the geodesic curvature is zero for an equilibrium configuration that is
uniform in poloidal direction. Note that this formula for 