In experiments, the beam emission spectroscopy (BES) and microwave
reflectometer can measure electron density fluctuation. The electron cyclotron
emission (ECE) radiometer can measure electron temperature fluctuation. In the
ideal MHD theory, we assume that
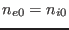 ,
,
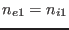 , and
the mass density is given approximately by
, and
the mass density is given approximately by
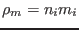 . Then the
linearized continuity equation,
. Then the
linearized continuity equation,
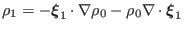 , is written as
, is written as
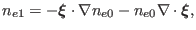 |
(307) |
which gives relationship between the density fluctuation and plasma
displacement. Similarly, in the ideal MHD theory, we assume that
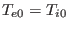 ,
,
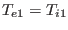 , and
, and
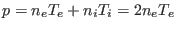 . Then
the linearized equation of state,
. Then
the linearized equation of state,
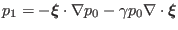 , is written as
, is written as
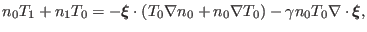 |
(308) |
Using Eq. () to eliminate 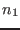 , Eq. () is written as
, Eq. () is written as
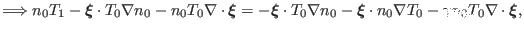 |
(309) |
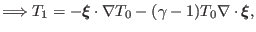 |
(310) |
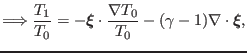 |
(311) |
The continuity equation is written as
 |
(312) |
Neglecting the compressible term, the above equation is written as
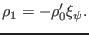 |
(313) |
Using
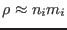 and
and 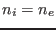 , the above equation is written as
, the above equation is written as
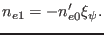 |
(314) |
Equation (314) relates the radial displacement obtained from a
eigenvalue code with the density perturbation 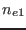 , which can be measured
by the reflectometer in experiments.
, which can be measured
by the reflectometer in experiments.
We know that the radial plasma displacement
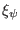 is related to the
perturbed thermal pressure through the relation:
is related to the
perturbed thermal pressure through the relation:
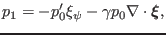 |
(315) |
Neglecting the compressible term, the above equation is written as
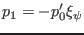 |
(316) |
yj
2015-09-04
![]() ,
,
![]() , and
the mass density is given approximately by
, and
the mass density is given approximately by
![]() . Then the
linearized continuity equation,
. Then the
linearized continuity equation,
![]() , is written as
, is written as
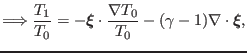
![]() is related to the
perturbed thermal pressure through the relation:
is related to the
perturbed thermal pressure through the relation: