Next, we derive the expression for the parallel and poloidal wave-number of a
perturbation of the form
![$\displaystyle \delta A = \delta A_0 (\psi) \exp [i (m \theta - n \zeta - \omega t)],$](img888.png) |
(317) |
where
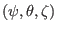 are the flux coordinators, with
are the flux coordinators, with 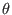 and
and
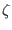 being the generalized poloidal and toroidal angles. The parallel (to
the local equilibrium magnetic field) wave vector,
being the generalized poloidal and toroidal angles. The parallel (to
the local equilibrium magnetic field) wave vector,
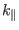 , is defined
by
, is defined
by
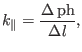 |
(318) |
where
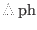 is the phase angle change of the perturbation when
moving a distance of
is the phase angle change of the perturbation when
moving a distance of 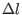 along the local equilibrium magnetic field.
According to Eq. (317), the phase change can be written as
along the local equilibrium magnetic field.
According to Eq. (317), the phase change can be written as
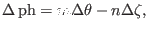 |
(319) |
where
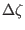 and
and
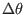 are the change in the toroidal and
poloidal angles when we move a distance of
are the change in the toroidal and
poloidal angles when we move a distance of 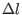 along the magnetic
field. Use Eq. (319) in Eq. (318), giving
along the magnetic
field. Use Eq. (319) in Eq. (318), giving
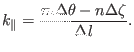 |
(320) |
Noting that the safety factor is given by
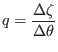 |
(321) |
(which is exact since we are using flux coordinator, in which magnetic field
lines are straight on
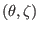 plane), Eq. (320) is written
as
plane), Eq. (320) is written
as
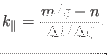 |
(322) |
In the approximation of large aspect ratio, 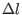 can be approximated by
can be approximated by
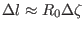 , where
, where 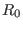 is the major radius of the
magnetic axis. Using this, the above equation is written as
is the major radius of the
magnetic axis. Using this, the above equation is written as
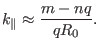 |
(323) |
(Remarks: I should use the exact expression for 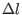 to derive an exact
expression for
to derive an exact
expression for
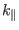 , I will do this later.) Equation (323)
indicates that
, I will do this later.) Equation (323)
indicates that
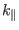 is zero on the resonant surface.
is zero on the resonant surface.
Similarly, the component of the wave vector along the 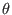 direction is
written as
direction is
written as
where
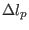 is the poloidal arc length when the poloidal angle changes
by
is the poloidal arc length when the poloidal angle changes
by
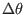 . If the equal-arc poloidal angle is used, then
. If the equal-arc poloidal angle is used, then
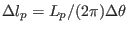 , where
, where 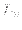 is the poloidal circumference of
the magnetic surface. Using this, Eq. (324) is written as
is the poloidal circumference of
the magnetic surface. Using this, Eq. (324) is written as
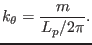 |
(325) |
If a circular flux surface is assumed, then the above equation is written as
where 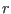 is the radius of the flux surface.
is the radius of the flux surface.
yj
2015-09-04
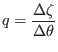
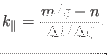
![]() direction is
written as
direction is
written as