5.1 Vlasov equation

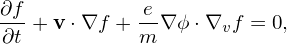
Consider the electrostatic case. The Vlasov equation (??) for electrons is written

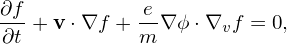(73)

where ϕ is the electric potential. Consider the one-dimensional case where f and ϕ are independent of y and z coordinates. In this case, the above equation is written

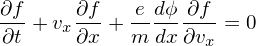(74)

Integrating both sides of the above equation over v_y and v_z, we obtain

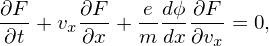(75)

where F(x,v_x,t) = ∫ _−∞^∞∫ _−∞^∞fdv_ydv_z is the reduced distribution function. Define characteristic lines by the following ordinary differential equations:

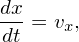(76)

and

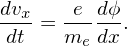(77)

Then along a characteristic line, we obtain

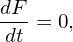(78)

which indicates that the distribution function F remain unchanged along a characteristic line.