5.8 Evaluation of particle number density

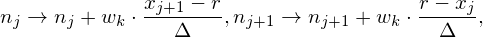
Set up uniform grid-points in x-direction: x_j = jΔ for j = 0,1,2,…,N, as is shown in Fig. 3. Use the first b-spline (flat-top function) with a support Δ_p = Δ as the shape function of markers. It is obvious that we can use the following procedures to obtain the number of physical particles in each cell. For a particle marker labeled by k whose position is x = r, we can find which two grids the particle lies between. Suppose that r is between x_j and x_j+1, then the particle number n_j and n_j+1 is evaluated as follows

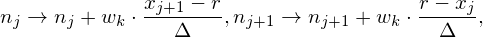(99)

where w_k is the weight of the marker. Performing the same procedures for each marker in turn allows us to build up n_j at all the grid points (all n_j are set to zero before these procedures).

The particle number at the boundary grid-points j = 0 and j = N needs special treatment. The above treatment do not include the contribution to n₀ from the left cell of the j = 0. Since we use periodic boundary condition, the contribution to n₀ from the left cell of the j = 0 grid is identical to the contribution to n_N from the left cell of the j = N grid. The latter has already been calculated in the above, which can be added to n₀ obtained above to get the final n₀. The same situation applies for n_N. After these treatment, we have n₀ = n_N.

Dividing the particle number n_j by the cell size Δ gives the number density.