Finite diﬀerence solver for Poisson equation

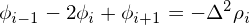
Using the center diﬀerence scheme for the second order derivative, the discrete form of Eq. (100) is written

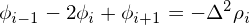ϕi− 1 − 2ϕi + ϕi+1 = − Δ2ρi

(114)

Using the boundary condition ϕ₀ = ϕ_N−1 = 0, equation (114) is written in the following tridiagonal matrix form:

A ϕ = b

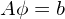(115)

where

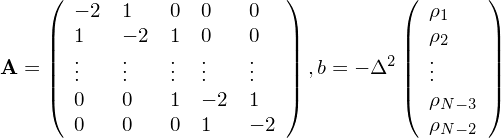( − 2 1 0 0 0 ) ( ρ ) | 1 − 2 1 0 0 | | ρ1 | || . . . . . || 2 || .2 || A = || .. .. .. .. .. || ,b = − Δ || .. || ( 0 0 1 − 2 1 ) ( ρN −3 ) 0 0 0 1 − 2 ρN −2

(116)

The results presented in this note are obtained by using the FFT solver, instead of the ﬁnite diﬀerence solver.