[next] [tail] [up]

7.1 Uniformly distributed random number

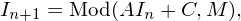
Generating random numbers that are uniform distributed in the range [0,1] is the basis for generating non-uniform distribution. Because the same program with the same input always produces the same output, it is not possible to write a program that produces truly random numbers. However, for most purposes, a pseudo-random number sequence will work almost as well. By “pseudo-random number”, we mean a repeatable sequence of numbers that has statistical properties similar to a random sequence. The most well-known algorithm for generating pseudo-random sequences of integers is the linear congruental method[4], in which the nth and (n + 1)th integers in the sequence is related by

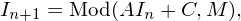In+1 = Mod (AIn + C,M ),
(134)

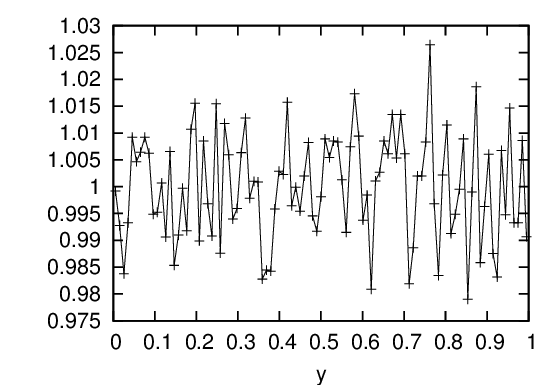
where Mod is the remainder function, A, C, and M are positive integer constants. The first number in the sequence, which is called the seed value, is selected by users. Equation (134) can generate pseudo-random number that is uniform distributed in the range [0,M − 1]. The obtained sequence can be scaled by a factor of M − 1 to lie in the range [0,1]. Figure 12 plots the possibility density of 106 values returned by Eq. (134)  with parameters A = 16807, C = 0, M = 2147483647 (this choice is called the Park and Miller method). In practice we need to use Schrange’s algorithm to avoid integer overflow[4].

pict

Figure 12: The distribution of the 106 values returned by the the random number generator Eq. (134). The possibility density (value of the distribution function) is obtained by the following steps: (1) divide the range [0,1] into 100 sub-regions; (2) then counts respectively the number of the returned value whose values are in the sub-regions; (3) the numbers of value in each sub-region obtained this way is further divided by the total number of values (106) to give the relativistic possibilities; (4) scale the relativistic possibilities by 100 times, which gives the exact possibility density (this scaling is needed because the sub-region is of length 1∕100, instead of unit length). Note that the value of the possibility density can be larger than one.

 

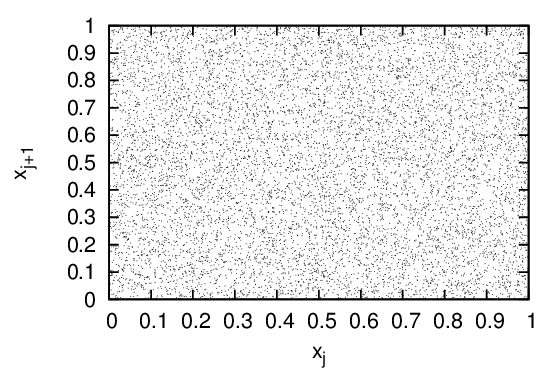
Another way to visualize whether the values generated by the random generator are random distributed in the region [0,1] is to view how the points (xj,xj+1) are distributed in the two-dimension plane, as is plotted in Fig. 13.

pict

Figure 13: Plot of xj verse xj+1 for j = 1,2,…,104. Here xj are random numbers generated by the random number generator.

[next] [front] [up]