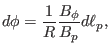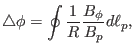Expression of safety factor in terms of magnetic field

The equation of magnetic field lines is given by

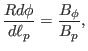$$\frac{R d \phi}{d \ell_p} = \frac{B_{\phi}}{B_p},$$ (26)

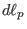where $d \ell_p$ is the line element along the direction of 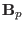$\mathbf{B}_p$ on the poloidal plane. Equation (26) can be arranged in the form

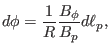$$d \phi = \frac{1}{R} \frac{B_{\phi}}{B_p} d \ell_p,$$ (27)

which can be integrated over 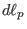$d \ell_p$ to give

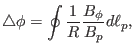$$\triangle \phi = \oint \frac{1}{R} \frac{B_{\phi}}{B_p} d \ell_p,$$ (28)

where the line integration is along the poloidal magnetic field (the contour of $\Psi$ on the poloidal plane). Using this, Eq. (25) is written

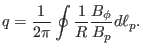$$q = \frac{1}{2 \pi} \oint \frac{1}{R} \frac{B_{\phi}}{B_p} d \ell_p .$$ (29)

The safety factor characterizes the average pitch angle of magnetic field lines on closed magnetic surfaces.