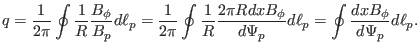The safety factor given by Eq. (29) is expressed in terms of the
components of the magnetic field. The safety factor can also be expressed in
terms of the magnetic flux. Define  as the poloidal magnetic flux
enclosed by two neighboring closed magnetic surface, then
as the poloidal magnetic flux
enclosed by two neighboring closed magnetic surface, then  can be
written
can be
written
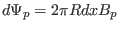 |
(30) |
where 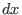 is perpendicular to the first magnetic surface (so perpendicular
to the
is perpendicular to the first magnetic surface (so perpendicular
to the
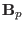 ) and its length is equal to the length from the point on
this magnetic surface to the point on the neighbour magnetic surface. Using
Eq. (30), the poloidal magnetic field is written as
) and its length is equal to the length from the point on
this magnetic surface to the point on the neighbour magnetic surface. Using
Eq. (30), the poloidal magnetic field is written as
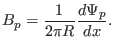 |
(31) |
Substituting Eq. (31) into Eq. (29), we obtain
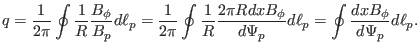 |
(32) |
We know 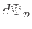 is a constant independent of the poloidal location, so
is a constant independent of the poloidal location, so 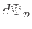 can be taken outside the integration to give
can be taken outside the integration to give
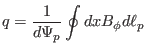 |
(33) |
On the other hand, the toroidal magnetic flux enclosed by the two magnetic
surfaces, 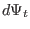 , is given by
, is given by
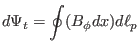 |
(34) |
Using this, Eq. (33) is written as
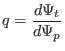 |
(35) |
Equation (35) indicates that the safety factor of a magnetic surface
is equal to the differential of the toroidal magnetic flux with respect to the
poloidal magnetic flux enclosed by the magnetic surface.
yj
2018-03-09
![]() as the poloidal magnetic flux
enclosed by two neighboring closed magnetic surface, then
as the poloidal magnetic flux
enclosed by two neighboring closed magnetic surface, then ![]() can be
written
can be
written