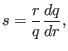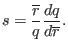The normalized pressure gradient,  , which appears frequently in
tokamak literature, is defined by[2]
, which appears frequently in
tokamak literature, is defined by[2]
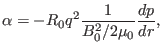 |
(504) |
which can be further written
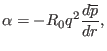 |
(505) |
where
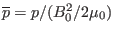 . Equation (505) can be
further written as
. Equation (505) can be
further written as
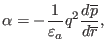 |
(506) |
where
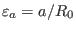 ,
,
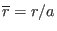 , and
, and 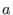 is the minor
radius of the boundary flux surface. (Why is there a
is the minor
radius of the boundary flux surface. (Why is there a 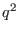 factor in the
definition of
factor in the
definition of  ?)
?)
The global magnetic shear 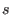 is defined by
is defined by
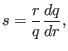 |
(507) |
which can be written
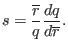 |
(508) |
In the case of large aspect ratio and circular flux surface, the leading order
equation of the Grad-Shafranov equation in
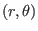 coordinates is
written
coordinates is
written
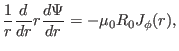 |
(509) |
which gives concentric circular flux surfaces centered at
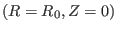 .
Assume that
.
Assume that 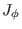 is uniform distributed, i.e.,
is uniform distributed, i.e.,
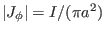 , where
, where 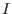 is the total current within the flux surface
is the total current within the flux surface 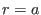 . Further
assume the current is in the opposite direction of
. Further
assume the current is in the opposite direction of
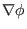 , then
, then
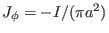 . Using this, Eq. (509) can be solved
to give
. Using this, Eq. (509) can be solved
to give
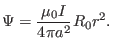 |
(510) |
Then it follows that the normalized radial coordinate
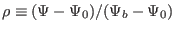 relates to
relates to
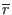 by
by
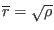 (I check this numerically for the case of EAST discharge
#38300). Sine in my code, the radial coordinate is
(I check this numerically for the case of EAST discharge
#38300). Sine in my code, the radial coordinate is  , I need to
transform the derivative with respect to
, I need to
transform the derivative with respect to
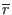 to one with respect to
to one with respect to
 , which gives
, which gives
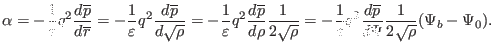 |
(511) |
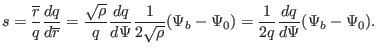 |
(512) |
The necessary condition for the existence of TAEs with frequency near the
upper tip of the gap is given by[2]
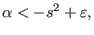 |
(513) |
which is used in my paper on Alfvén eigenmodes on EAST
tokamak[8]. Equations (511) and (512) are used in
the GTAW code to calculate 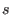 and
and  .
.
yj
2018-03-09
![]() , which appears frequently in
tokamak literature, is defined by[2]
, which appears frequently in
tokamak literature, is defined by[2]
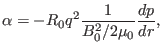
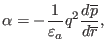
![]() is defined by
is defined by