Using Ampere's circuital law
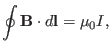 |
(514) |
along the toroidal direction and assuming perfect toroidal symmetry, Eq.
(514) is written
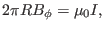 |
(515) |
which gives
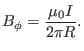 |
(516) |
Neglecting the poloidal current contributed by the plasma, the poloidal
current is determined solely by the current in the TF (Toroidal Field) coils.
The EAST tokamak has 16 groups of TF coils, with each coils having 130 turns
of wire (I got to know the number of turns from Dr. Sun Youwen). Denote the
current in a single turn by 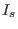 , then Eq. (516) is written
, then Eq. (516) is written
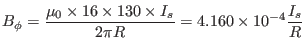 |
(517) |
Using this formula, the strength of the toroidal magnetic field at 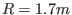 for
for
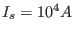 is calculated to be
is calculated to be
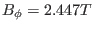 . This field (
. This field (
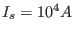 , and thus
, and thus
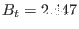 at
at 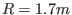 ) was chosen as one of the two
scenarios of EAST experiments during 2014/6-2014/9 (another scenario is
) was chosen as one of the two
scenarios of EAST experiments during 2014/6-2014/9 (another scenario is
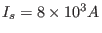 ). (The limit of the current in a single turn of the TF coils
is
). (The limit of the current in a single turn of the TF coils
is
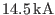 (from B. J. Xiao's paper [13]).
(from B. J. Xiao's paper [13]).
Note that the exact equilibrium toroidal magnetic field 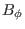 is given by
is given by
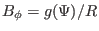 . Compare this with Eq. (516), we know that
the approximation made to obtain Eq. (517) is equivalent to
. Compare this with Eq. (516), we know that
the approximation made to obtain Eq. (517) is equivalent to
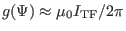 , i.e. assuming
, i.e. assuming 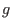 is a constant function
of
is a constant function
of  . The poloidal plasma current density is related to
. The poloidal plasma current density is related to 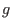 by
by
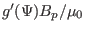 . The constant
. The constant 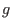 corresponds to zero plasma poloidal current,
which is consistent to the assumption used to obtain Eq. (517).
corresponds to zero plasma poloidal current,
which is consistent to the assumption used to obtain Eq. (517).
yj
2018-03-09
![]() is given by
is given by
![]() . Compare this with Eq. (516), we know that
the approximation made to obtain Eq. (517) is equivalent to
. Compare this with Eq. (516), we know that
the approximation made to obtain Eq. (517) is equivalent to
![]() , i.e. assuming
, i.e. assuming ![]() is a constant function
of
is a constant function
of ![]() . The poloidal plasma current density is related to
. The poloidal plasma current density is related to ![]() by
by
![]() . The constant
. The constant ![]() corresponds to zero plasma poloidal current,
which is consistent to the assumption used to obtain Eq. (517).
corresponds to zero plasma poloidal current,
which is consistent to the assumption used to obtain Eq. (517).