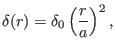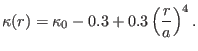According to Refs. [5,10], Miller's formula for a series
of shaped flux surfaces is given by
![$\displaystyle R = R_0 (r) + r \cos \{ \theta + \arcsin [\delta (r) \sin \theta] \},$](img1489.png) |
(518) |
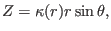 |
(519) |
where
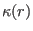 and
and
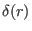 are elongation and triangularity profile,
are elongation and triangularity profile,
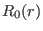 is the Shafranov shift profile, which is given by
is the Shafranov shift profile, which is given by
![$\displaystyle R_0 (r) = R_0 (a) - \frac{a R_0'}{2} \left[ 1 - \left( \frac{r}{a} \right)^2 \right],$](img1494.png) |
(520) |
where 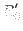 is a constant,
is a constant, 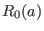 is the major radius of the center of the
boundary flux surface. The triangularity profile is
is the major radius of the center of the
boundary flux surface. The triangularity profile is
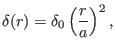 |
(521) |
and the elongation profile is
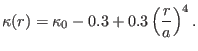 |
(522) |
The nominal ITER parameters are
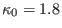 ,
,
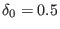 and
and
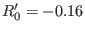 . I wrote a code to plot the shapes of the flux surface
(/home/yj/project/miller_flux_surface). An example of the results is given
in Fig. 33.
. I wrote a code to plot the shapes of the flux surface
(/home/yj/project/miller_flux_surface). An example of the results is given
in Fig. 33.
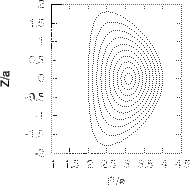
Figure 33:
Flux-surfaces given by Eqs. (518) and
(519) with 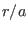 varying from 0.1 to 1.0 (corresponding boundary
surface). Other parameters are
varying from 0.1 to 1.0 (corresponding boundary
surface). Other parameters are
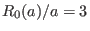 ,
,
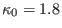 ,
,
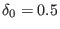 ,
,
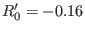 .
.
 |
yj
2018-03-09
![$\displaystyle R_0 (r) = R_0 (a) - \frac{a R_0'}{2} \left[ 1 - \left( \frac{r}{a} \right)^2 \right],$](img1494.png)