An analytic expression for the pressure profile of double (inner and external)
transport barriers is given by
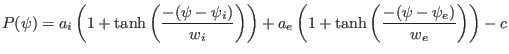 |
(523) |
where 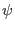 is the normalized poloidal flux,
is the normalized poloidal flux, 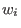 and
and 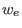 are the width of
the inner and external barriers,
are the width of
the inner and external barriers, 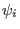 and
and 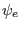 are the locations of
the barriers,
are the locations of
the barriers, 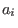 and
and 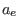 is the height of the barriers,
is the height of the barriers, 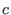 is a constant
to ensure
is a constant
to ensure
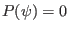 at
at 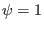 .
.
Figure 34:
Pressure profile of double (inner and external) transport barriers
given by Eq. (523) with 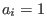 ,
, 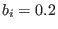 ,
,
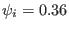 ,
,
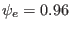 ,
, 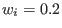 ,
,
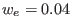 ,
, 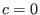 .
.
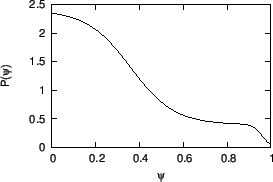 |
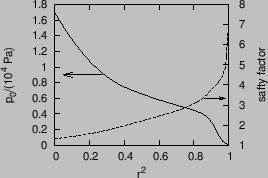
Figure 35:
Equilibrium pressure profile for EAST discharge #38300 at 3.9s
(reconstructed by EFIT code, gfile name: g038300.03900), which shows a
boundary transport barrier.
 |
yj
2018-03-09

