Next: tmp check! Up: Misc contents Previous: Ballooning transformation
Note that, on both an irrational surface and a rational surface, there are
infinite number of magnetic field lines that are not connected with each other
(it is wrong to say there is only one magnetic field line on a irrational
surface). Sine
![]() , the value
, the value ![]() is a
constant along any one of the magnetic field lines. Now comes the question:
whether the values of
is a
constant along any one of the magnetic field lines. Now comes the question:
whether the values of ![]() on different field lines are equal to each other?
To answer this question, we can choose a direction different from
on different field lines are equal to each other?
To answer this question, we can choose a direction different from
![]() on the magnetic surface and examine whether
on the magnetic surface and examine whether ![]() is constant or not along
this direction, i.e, whether
is constant or not along
this direction, i.e, whether
![]() equals zero or
not, where
equals zero or
not, where
![]() is the chosen direction. For axsiymmetric magnetic
surfaces, it is ready to see that
is the chosen direction. For axsiymmetric magnetic
surfaces, it is ready to see that
![]() is a
direction on the magnetic surface and it is usually not identical with
is a
direction on the magnetic surface and it is usually not identical with
![]() . Then we obtain
. Then we obtain
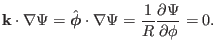 |
(527) |
[check***As discussed in Sec. 2.1, the force balance equation of
axisymmetric plasma requires that
![]() . From this
and the fact
. From this
and the fact
![]() , we conclude that
, we conclude that ![]() is a
function of
is a
function of ![]() , i.e.,
, i.e.,
![]() . However, this reasoning is not
rigorous. Note the concept of a function requires that a function can not be a
one-to-more map. This means that
. However, this reasoning is not
rigorous. Note the concept of a function requires that a function can not be a
one-to-more map. This means that
![]() indicates that the values of
indicates that the values of
![]() must be equal on two different magnetic field lines that have the same
value of
must be equal on two different magnetic field lines that have the same
value of ![]() . However, the two equations
. However, the two equations
![]() and
and
![]() do not require this constraint. To
examine whether this constraint removes some equilibria from all the possible
ones, we consider a system with an
do not require this constraint. To
examine whether this constraint removes some equilibria from all the possible
ones, we consider a system with an ![]() point. Inside one of the magnetic
islands, we use
point. Inside one of the magnetic
islands, we use
yj 2018-03-09