Next: Discussion about the poloidal Up: Misc contents Previous: Double transport barriers pressure
To construct a periodic function about ![]() , we introduces a function
, we introduces a function
![]() which is defined over
which is defined over
![]() and
vanishes sufficiently fast as
and
vanishes sufficiently fast as
![]() so that the
following infinite summation converge:
so that the
following infinite summation converge:
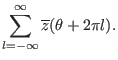 |
(524) |
| (526) |
If we use the right-hand-side of Eq. (525) to represent
![]() , then we do not need to worry about the periodic property of
, then we do not need to worry about the periodic property of
![]() (the periodic property is guaranteed by the representation)
(the periodic property is guaranteed by the representation)