Next: Plasma current density Up: Safety factor Previous: Expression of safety factor
If the safety factor of a magnetic surface is a rational number, i.e., ![]() , where
, where ![]() and
and ![]() are integers, then this magnetic surface is called a
rational surface, otherwise an irrational surface. It is obvious that a field
line on a rational surface with
are integers, then this magnetic surface is called a
rational surface, otherwise an irrational surface. It is obvious that a field
line on a rational surface with ![]() closes itself after traveling
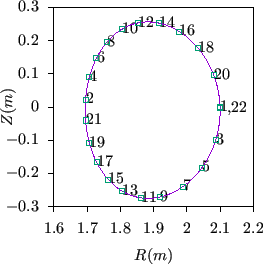
closes itself after traveling ![]() toroidal turns and
toroidal turns and ![]() poloidal turns. An example of a magnetic field line on
a rational surface is shown in Fig. 5.
poloidal turns. An example of a magnetic field line on
a rational surface is shown in Fig. 5.
  |
yj 2018-03-09