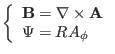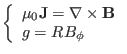Relation of 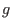 with the poloidal electric current
with the poloidal electric current
As is discussed in Sec. 2.1, to satisfy the force balance in the
toroidal direction,
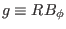 must be a magnetic surface function,
i.e.,
must be a magnetic surface function,
i.e.,
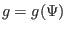 . Using this, equations (37) and (38)
are written
. Using this, equations (37) and (38)
are written
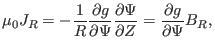 |
(57) |
and
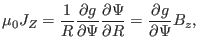 |
(58) |
respectively. The above two equations imply that
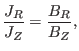 |
(59) |
which implies that the projections of
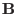 lines and
lines and
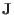 lines on the poloidal plane are identical to each other. This indicates that
the
lines on the poloidal plane are identical to each other. This indicates that
the
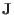 surfaces coincide with the magnetic surfaces. Using this and
surfaces coincide with the magnetic surfaces. Using this and
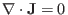 , and following the same steps in Sec.
1.4, we obtain
, and following the same steps in Sec.
1.4, we obtain
![$\displaystyle I_{\ensuremath{\operatorname{pol}}} = \frac{1}{\mu_0} 2 \pi [g (\Psi_2) - g (\Psi_1)],$](img280.png) |
(60) |
where
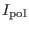 is the poloidal current enclosed by the two magnetic
surfaces, the positive direction of
is the poloidal current enclosed by the two magnetic
surfaces, the positive direction of
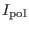 is chosen to be in the
clockwise direction when observers look along
is chosen to be in the
clockwise direction when observers look along
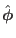 .
Equation (60) indicates that the difference of
.
Equation (60) indicates that the difference of 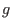 between two
magnetic surface is proportional to the poloidal current. For this reason,
between two
magnetic surface is proportional to the poloidal current. For this reason, 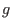 is usually call the ``poloidal current function''.
is usually call the ``poloidal current function''.
In the above, we see that the relation of 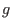 with the poloidal electric
current is similar to that of
with the poloidal electric
current is similar to that of  with the poloidal magnetic flux. This
similarity is due to the following differential relations:
with the poloidal magnetic flux. This
similarity is due to the following differential relations:
yj
2018-03-09
![]() must be a magnetic surface function,
i.e.,
must be a magnetic surface function,
i.e.,
![]() . Using this, equations (37) and (38)
are written
. Using this, equations (37) and (38)
are written
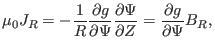
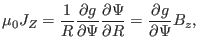
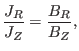
![]() with the poloidal electric
current is similar to that of
with the poloidal electric
current is similar to that of ![]() with the poloidal magnetic flux. This
similarity is due to the following differential relations:
with the poloidal magnetic flux. This
similarity is due to the following differential relations: