Next: Example: () coordinates Up: Curvilinear coordinate system Previous: Coordinates transformation and Jacobian
Next, we shall prove the following orthogonality relation
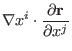 |
![$\displaystyle \left[
\left( \frac{\partial x^i}{\partial x} \right) \hat{\mathb...
...^j} \hat{\mathbf{z}} + z \frac{\partial
\hat{\mathbf{z}}}{\partial x^j} \right]$](img435.png) |
||
![$\displaystyle \left[ \left( \frac{\partial x^i}{\partial x} \right)
\hat{\mathb...
...^j} \hat{\mathbf{y}} +
\frac{\partial z}{\partial x^j} \hat{\mathbf{z}} \right]$](img436.png) |
|||
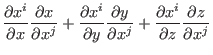 |
|||
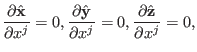 |
(107) |
It can be proved that
![]() is a contravariant vector while
is a contravariant vector while
![]() is a covariant vector (I do not prove this). The
orthogonality relation in Eq. (106) is fundamental to the theory of
general coordinates. (The cylindrical coordinate system
is a covariant vector (I do not prove this). The
orthogonality relation in Eq. (106) is fundamental to the theory of
general coordinates. (The cylindrical coordinate system
![]() is an
example of general coordinates. As an exercise, we can verify that the
cylindrical coordinates have the above property. In this case,
is an
example of general coordinates. As an exercise, we can verify that the
cylindrical coordinates have the above property. In this case,
![]() ,
,
![]() ,
, ![]() , where
, where
![]() ,
,
![]() ,
,
![]() .) The orthogonality relation allows one to write the covariant
basis vectors in terms of contravariant basis vectors and vice versa. For
example, the orthogonality relation tells that
.) The orthogonality relation allows one to write the covariant
basis vectors in terms of contravariant basis vectors and vice versa. For
example, the orthogonality relation tells that
![]() is orthogonal to
is orthogonal to
![]() and
and
![]() , thus,
, thus,
![]() can be written as
can be written as
| (109) |
| (110) |
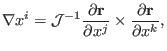 |
(115) |
yj 2018-03-09