Suppose
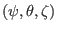 is an arbitrary general coordinate system.
Then the covariant basis vectors are
is an arbitrary general coordinate system.
Then the covariant basis vectors are
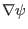 ,
,
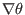 , and
, and
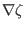 , and the corresponding contravariant basis vectors are written
as
, and the corresponding contravariant basis vectors are written
as
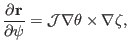 |
(116) |
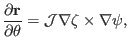 |
(117) |
and
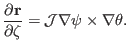 |
(118) |
In Einstein notation, contravariant basis vectors are denoted with upper
indices as
and the covariant basis vectors are denoted with low indices as
Then the orthogonality relation, Eq. (106), is written as
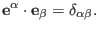 |
(120) |
Then, in term of the contravairant basis vectors,
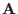 is written
is written
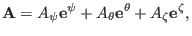 |
(121) |
where
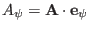 ,
,
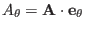 , and
, and
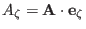 . Similarly, in term of the covariant basis vectors,
. Similarly, in term of the covariant basis vectors,
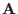 is written
is written
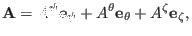 |
(122) |
where
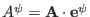 ,
,
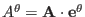 , and
, and
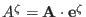 .
.
[In passing, we note that
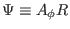 is the covariant toroidal
component of
is the covariant toroidal
component of
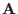 in cylindrical coordinates
in cylindrical coordinates
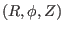 . The proof
is as follows. Note that the covariant form of
. The proof
is as follows. Note that the covariant form of
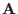 should be
expressed in terms of the contravariant basis vector (
should be
expressed in terms of the contravariant basis vector (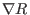 ,
,
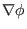 , and
, and 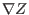 ), i.e.,
), i.e.,
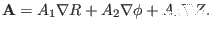 |
(123) |
where 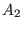 is the covariant toroidal component of
is the covariant toroidal component of
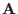 . To obtain
. To obtain
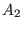 , we take scalar product of Eq. (123) with
, we take scalar product of Eq. (123) with
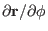 and use the orthogonality relation (106),
which gives
and use the orthogonality relation (106),
which gives
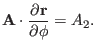 |
(124) |
In cylindrical coordinates
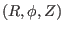 , the location vector is written as
, the location vector is written as
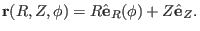 |
(125) |
Using this, we obtain
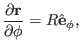 |
(126) |
Use Eq. (126) in Eq. (124) giving
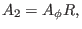 |
(127) |
which indicates that
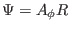 is the covariant toroidal component
of the vector potential.]
is the covariant toroidal component
of the vector potential.]
yj
2018-03-09
![]() is an arbitrary general coordinate system.
Then the covariant basis vectors are
is an arbitrary general coordinate system.
Then the covariant basis vectors are
![]() ,
,
![]() , and
, and
![]() , and the corresponding contravariant basis vectors are written
as
, and the corresponding contravariant basis vectors are written
as
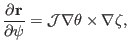
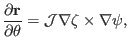
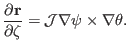
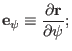
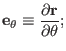
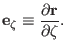
![]() is the covariant toroidal
component of
is the covariant toroidal
component of
![]() in cylindrical coordinates
in cylindrical coordinates
![]() . The proof
is as follows. Note that the covariant form of
. The proof
is as follows. Note that the covariant form of
![]() should be
expressed in terms of the contravariant basis vector (
should be
expressed in terms of the contravariant basis vector (![]() ,
,
![]() , and
, and ![]() ), i.e.,
), i.e.,