Relation between Jacobian and poloidal angle
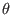
In
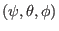 coordinates, a line element is written
coordinates, a line element is written
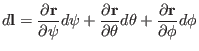 |
(185) |
The line element that lies on a magnetic surface (i.e.,
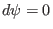 ) and on a
poloidal plane (i.e.,
) and on a
poloidal plane (i.e.,
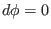 ) is then written
) is then written
We use the convention that 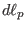 and
and 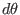 take the same sign, i.e.,
take the same sign, i.e.,
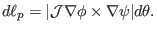 |
(187) |
Using the fact that
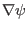 and
and
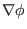 is orthogonal and
is orthogonal and
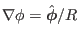 , the above equation is written as
, the above equation is written as
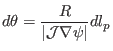 |
(188) |
Given
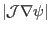 , Eq. (188) can be used to
determine the
, Eq. (188) can be used to
determine the 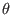 coordinate of points on a magnetic surface.
coordinate of points on a magnetic surface.
yj
2018-03-09
![]() coordinates, a line element is written
coordinates, a line element is written