Normalized poloidal coordinate
The range of  defined by Eq. (189) is usually not within
defined by Eq. (189) is usually not within
![$ [0
: 2 \pi]$](img613.png) . Define a normalized poloidal coordinate
. Define a normalized poloidal coordinate
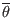 by
by
which is obviously within the range
![$ [0
: 2 \pi]$](img613.png) . Sine we have modified the
definition of the poloidal angle, the Jacobian of the new coordinates
. Sine we have modified the
definition of the poloidal angle, the Jacobian of the new coordinates
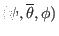 is different from that of
is different from that of
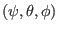 .
Next, we determine the Jacobian
.
Next, we determine the Jacobian
 of the new
coordinates
of the new
coordinates
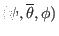 . Equation (191) can
be written as
. Equation (191) can
be written as
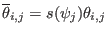 with
with
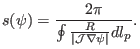 |
(192) |
The Jacobian
 of the new coordinates system
of the new coordinates system
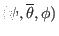 is written
is written
The Jacobian
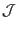 can be set to various forms to achieve desired
poloidal coordinates (as given in the next section). After the radial
coordinate
can be set to various forms to achieve desired
poloidal coordinates (as given in the next section). After the radial
coordinate 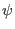 is chosen, all the quantities on the right-hand side of Eq.
(191) are known and the integration can be performed to obtain the
value of
is chosen, all the quantities on the right-hand side of Eq.
(191) are known and the integration can be performed to obtain the
value of  of each point on each flux surface.
of each point on each flux surface.
yj
2018-03-09
![]() defined by Eq. (189) is usually not within
defined by Eq. (189) is usually not within
![]() . Define a normalized poloidal coordinate
. Define a normalized poloidal coordinate
![]() by
by