If the Jacobian
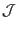 is chosen to be of the following form
is chosen to be of the following form
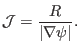 |
(194) |
Then
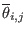 in Eq. (191) is written
in Eq. (191) is written
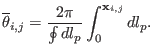 |
(195) |
and the Jacobian
 given by Eq. (193) now
takes the form
given by Eq. (193) now
takes the form
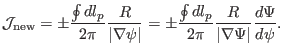 |
(196) |
Equation (195) indicates a set of poloidal points with equal arc
intervals corresponds to a set of uniform 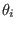 points. Therefore this
choice of the Jacobian is called the equal-arc-length Jacobian. Note that Eq.
(195) does not involve the radial coordinate
points. Therefore this
choice of the Jacobian is called the equal-arc-length Jacobian. Note that Eq.
(195) does not involve the radial coordinate 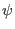 . Therefore the
values of
. Therefore the
values of  of points on any magnetic surface can be determined before
the radial coordinate is chosen. By using Eq. (195) (to calculate
of points on any magnetic surface can be determined before
the radial coordinate is chosen. By using Eq. (195) (to calculate
 ) and the definition of
) and the definition of 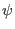 (to calculate
(to calculate 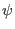 ), we obtain a
magnetic surface coordinate system
), we obtain a
magnetic surface coordinate system
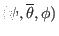 .
.
yj
2018-03-09
![]() is chosen to be of the following form
is chosen to be of the following form