Next, we discuss a new poloidal angle often used in the tearing mode theory,
which is defined by
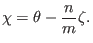 |
(261) |
Then it is ready to verify that the Jacobian of
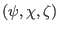 coordinates is equal to that of
coordinates is equal to that of
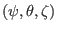 coordinates [proof:
coordinates [proof:
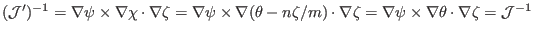 ]. The
component of
]. The
component of
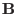 along
along
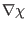 direction (a covariant
component) is written
direction (a covariant
component) is written
At the resonant surface 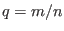 , Eq. (262) implies
, Eq. (262) implies
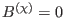 . On the other hand, the covariant component of
. On the other hand, the covariant component of
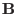 in
in  direction is written
direction is written
Using (263), equation (262) is written
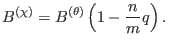 |
(264) |
In the cylindrical limit,
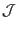 is a constant independent of the
poloidal angle. Then Eq. (263) indicates that
is a constant independent of the
poloidal angle. Then Eq. (263) indicates that
 is also
a constant on a magnetic surface.
is also
a constant on a magnetic surface.
yj
2018-03-09