Next: Form of operator in Up: Magnetic surface coordinates general Previous: Poloidal angle used in
In the above, we have given the covariant form of the magnetic field in
![]() coordinates (i.e., Eq. (177)). Next, we derive
the corresponding form in
coordinates (i.e., Eq. (177)). Next, we derive
the corresponding form in
![]() coordinate. In order to do
this, we need to express the
coordinate. In order to do
this, we need to express the
![]() basis vector in terms of
basis vector in terms of
![]() ,
,
![]() , and
, and
![]() basis vectors. Using the definition
of the generalized toroidal angle, we obtain
basis vectors. Using the definition
of the generalized toroidal angle, we obtain
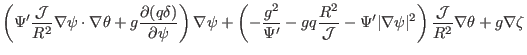 |
|||
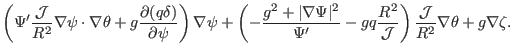 |
(267) |
yj 2018-03-09