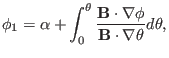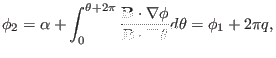Periodic conditions of physical quantity along 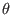 and
and
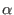 in field-line-following coordinates
in field-line-following coordinates
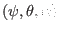
Since
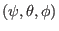 and
and
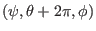 correspond to
the same spatial point, a general physical quantity
correspond to
the same spatial point, a general physical quantity 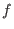 expressed in terms of
coordinates
expressed in terms of
coordinates
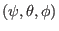 , i.e.,
, i.e.,
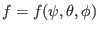 , must
satisfy the following periodic condtions along
, must
satisfy the following periodic condtions along 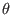 :
:
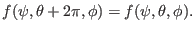 |
(285) |
Since
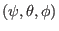 and
and
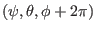 correspond to
the same spatial point,
correspond to
the same spatial point, 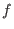 must satisfy the following periodic condtions
along
must satisfy the following periodic condtions
along 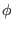 :
:
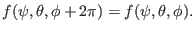 |
(286) |
Since
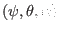 and
and
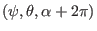 correspond
to the same spatial point, a general physical quantity
correspond
to the same spatial point, a general physical quantity 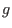 expressed in
field-line-following coordinates
expressed in
field-line-following coordinates
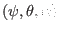 , i.e.,
, i.e.,
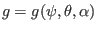 , must satisty the following peroidic condition along
, must satisty the following peroidic condition along
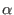 :
:
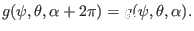 |
(287) |
However,
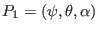 and
and
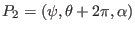 are not usually corresponding to the same spatial point. In fact,
equation (282) implies, for point
are not usually corresponding to the same spatial point. In fact,
equation (282) implies, for point 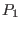 , its toroidal angle
, its toroidal angle
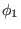 is given by
is given by
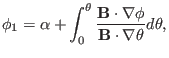 |
(288) |
while for point 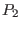 , its toroidal angle
, its toroidal angle 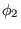 is given by
is given by
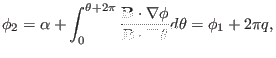 |
(289) |
i.e., 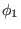 and
and 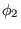 are different by
are different by 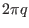 . From this, we know
that
. From this, we know
that
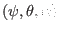 and
and
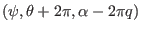 correspond to the same spatial point. Therefore we have the following periodic
condtion:
correspond to the same spatial point. Therefore we have the following periodic
condtion:
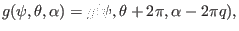 |
(290) |
which involves both 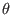 and
and 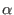 .
.
yj
2018-03-09
![]() and
and
![]() correspond to
the same spatial point, a general physical quantity
correspond to
the same spatial point, a general physical quantity ![]() expressed in terms of
coordinates
expressed in terms of
coordinates
![]() , i.e.,
, i.e.,
![]() , must
satisfy the following periodic condtions along
, must
satisfy the following periodic condtions along ![]() :
: