Next: Expression of metric elements Up: Field-line-following coordinates Previous: Some discussions
The generalized toroidal angle ![]() is numerically calculated in my code.
To verify
is numerically calculated in my code.
To verify
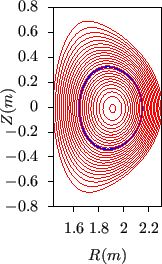
![]() along a magnetic field-line,
figure 26 plots the values of
along a magnetic field-line,
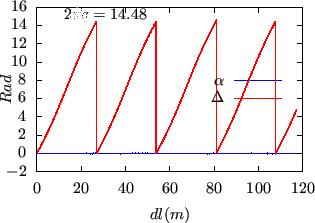
figure 26 plots the values of ![]() along a magnetic field
line, which indicates that
along a magnetic field
line, which indicates that ![]() is constant. This indicates the numerical
implementation of the field-aligned coordinates is correct.
is constant. This indicates the numerical
implementation of the field-aligned coordinates is correct.
  |