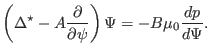In the GS equation, 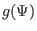 is one of the two free functions which can be
prescribed by users. In some cases, we want to specify the safety factor
profile
is one of the two free functions which can be
prescribed by users. In some cases, we want to specify the safety factor
profile 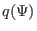 , instead of
, instead of 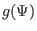 , in solving the GS equation. Next,
we derive the form of the GS equation that contains
, in solving the GS equation. Next,
we derive the form of the GS equation that contains 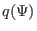 , instead of
, instead of 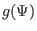 , as a free function. The safety factor defined in Eq. (182)
can be written
, as a free function. The safety factor defined in Eq. (182)
can be written
Equation (471) gives the relation between the safety factor 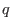 and
the toroidal field function
and
the toroidal field function 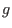 . This relation can be used in the GS equation
to eliminate
. This relation can be used in the GS equation
to eliminate 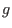 in favor of
in favor of 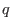 , which gives
, which gives
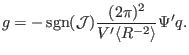 |
(472) |
![$\displaystyle \Rightarrow \frac{d g}{d \Psi} g = \frac{(2 \pi)^2}{V' \langle R^...
...e} q \left[ \frac{(2 \pi)^2}{V' \langle R^{- 2} \rangle} q \Psi' \right]_{\psi}$](img1400.png) |
(473) |
Multiplying Eq. (468) by 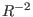 gives
gives
![$\displaystyle \frac{1}{\mathcal{J}} \left[ \left( \Psi' \frac{\mathcal{J}}{R^2}...
...{\theta} \right] + \mu_0 \frac{d p}{d \Psi} + R^{- 2} \frac{d g}{d \Psi} g = 0.$](img1402.png) |
(474) |
Surface-averaging the above equation, we obtain
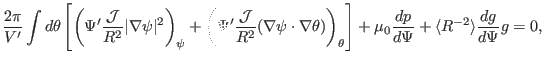 |
(475) |
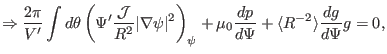 |
(476) |
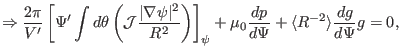 |
(477) |
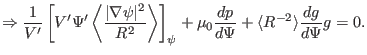 |
(478) |
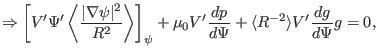 |
(479) |
Substitute Eq. (473) into the above equation to eliminate
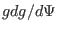 , we obtain
, we obtain
![$\displaystyle \Rightarrow \left[ V' \Psi' \left\langle \frac{\vert \nabla \psi ...
...(2 \pi)^4 \left[ \frac{q \Psi'}{V' \langle R^{- 2} \rangle} \right]_{\psi} = 0,$](img1409.png) |
(480) |
Eq. (480) agrees with Eq. (5.55) in Ref. [9].
![$\displaystyle \Rightarrow V' \left\langle \frac{\vert \nabla \psi \vert^2}{R^2}...
... (2 \pi)^4 \left[ \frac{q}{V' \langle R^{- 2} \rangle} \right]_{\psi} \Psi' = 0$](img1410.png) |
(481) |
![$\displaystyle \Rightarrow \Psi'' = - \frac{1}{V' D} \left\{ \left[ V' \left\lan...
...le R^{- 2} \rangle} \right]_{\psi} \Psi' + \mu_0 V' \frac{d p}{d \Psi} \right\}$](img1411.png) |
(482) |
where
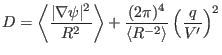 |
(483) |
The GS equation is
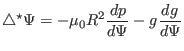 |
(484) |
![$\displaystyle \Rightarrow \triangle^{\star} \Psi = - \mu_0 R^2 \frac{d p}{d \Ps...
...{- 2} \rangle} \left[ \frac{q \Psi'}{V' \langle R^{- 2} \rangle} \right]_{\psi}$](img1414.png) |
(485) |
![$\displaystyle \Rightarrow \triangle^{\star} \Psi = - \mu_0 R^2 \frac{d p}{d \Ps...
...si} \Psi' + \left[ \frac{q}{V' \langle R^{- 2} \rangle} \right] \Psi'' \right\}$](img1415.png) |
(486) |
Using Eq. (482) to eliminate 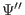 in the above equation, the
coefficients before (
in the above equation, the
coefficients before (
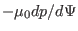 ) is written as
) is written as
Substituting the expression of 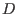 into the above equation, we obtain
into the above equation, we obtain
which is equal to the expression (5.58) in Ref. [9]. The
coefficient before 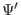 is written as
is written as
Define
![$\displaystyle \Longrightarrow \frac{D}{- (2 \pi)^4 \beta} A = D \beta_{\psi} - \beta \frac{1}{V'} [(V' \alpha)_{\psi} + q (2 \pi)^4 \beta_{\psi}]$](img1428.png) |
(489) |
![$\displaystyle \Longrightarrow \frac{D}{- \beta (2 \pi)^4} A = D \beta_{\psi} - \beta \frac{1}{V'} [V'' \alpha + V' \alpha_{\psi} + q (2 \pi)^4 \beta_{\psi}]$](img1429.png) |
(490) |
Using
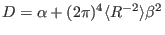 |
(491) |
Eq. () is written as
![$\displaystyle \left. \Longrightarrow \frac{D}{- \beta (2 \pi)^4} A = \alpha \be...
...c{1}{V'} V' \alpha_{\psi} - \beta \frac{1}{V'} q (2 \pi)^4 \beta_{\psi} \right]$](img1431.png) |
(492) |
![$\displaystyle \left. \Longrightarrow \frac{D}{- \beta (2 \pi)^4} A = \alpha \be...
...pha - \beta \alpha_{\psi} - \beta \frac{1}{V'} q (2 \pi)^4 \beta_{\psi} \right]$](img1432.png) |
(493) |
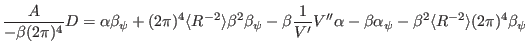 |
(494) |
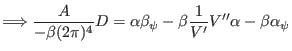 |
(495) |
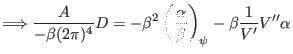 |
(496) |
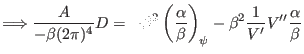 |
(497) |
![$\displaystyle \Longrightarrow \frac{A}{- \beta (2 \pi)^4} D = - \beta^2 \left[ ...
...c{\alpha}{\beta} \right)_{\psi} + \frac{1}{V'} V'' \frac{\alpha}{\beta} \right]$](img1437.png) |
(498) |
![$\displaystyle \Longrightarrow \frac{A}{- \beta (2 \pi)^4} D = - \beta^2 \frac{1...
...left( \frac{\alpha}{\beta} \right)_{\psi} V' + V'' \frac{\alpha}{\beta} \right]$](img1438.png) |
(499) |
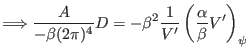 |
(500) |
![$\displaystyle \Longrightarrow A = \frac{(2 \pi)^4}{D} \left( \frac{q}{V' \langl...
...^2} \right\rangle \frac{\langle R^{- 2} \rangle}{q} V^{\prime 2} \right]_{\psi}$](img1440.png) |
(501) |
But the expression of 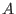 is slightly different from that given in Ref.
[9] [Eq. (5.57)]. Using the above coefficients, the GS
equation with the
is slightly different from that given in Ref.
[9] [Eq. (5.57)]. Using the above coefficients, the GS
equation with the 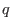 -profile held fixed is written as
-profile held fixed is written as
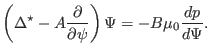 |
(502) |
yj
2018-03-09
![]() is one of the two free functions which can be
prescribed by users. In some cases, we want to specify the safety factor
profile
is one of the two free functions which can be
prescribed by users. In some cases, we want to specify the safety factor
profile ![]() , instead of
, instead of ![]() , in solving the GS equation. Next,
we derive the form of the GS equation that contains
, in solving the GS equation. Next,
we derive the form of the GS equation that contains ![]() , instead of
, instead of ![]() , as a free function. The safety factor defined in Eq. (182)
can be written
, as a free function. The safety factor defined in Eq. (182)
can be written
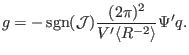
![$\displaystyle \frac{1}{\mathcal{J}} \left[ \left( \Psi' \frac{\mathcal{J}}{R^2}...
...{\theta} \right] + \mu_0 \frac{d p}{d \Psi} + R^{- 2} \frac{d g}{d \Psi} g = 0.$](img1402.png)
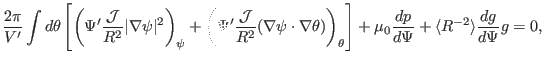
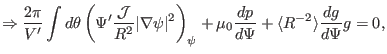
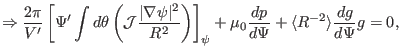
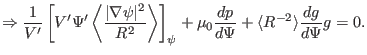
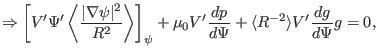
![$\displaystyle \Rightarrow V' \left\langle \frac{\vert \nabla \psi \vert^2}{R^2}...
... (2 \pi)^4 \left[ \frac{q}{V' \langle R^{- 2} \rangle} \right]_{\psi} \Psi' = 0$](img1410.png)
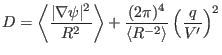
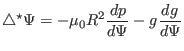
![$\displaystyle \Rightarrow \triangle^{\star} \Psi = - \mu_0 R^2 \frac{d p}{d \Ps...
...{- 2} \rangle} \left[ \frac{q \Psi'}{V' \langle R^{- 2} \rangle} \right]_{\psi}$](img1414.png)
![$\displaystyle \Rightarrow \triangle^{\star} \Psi = - \mu_0 R^2 \frac{d p}{d \Ps...
...si} \Psi' + \left[ \frac{q}{V' \langle R^{- 2} \rangle} \right] \Psi'' \right\}$](img1415.png)
![$\displaystyle R^2 - \frac{q (2 \pi)^4}{V' \langle R^{- 2} \rangle} \left\{ \left[
\frac{q}{V' \langle R^{- 2} \rangle} \right] \frac{1}{V' D} V' \right\}$](img1419.png)
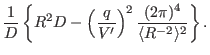
![$\displaystyle A = - \frac{q (2 \pi)^4}{V' \langle R^{- 2} \rangle} \left\{ \lef...
...4 \left[ \frac{q}{V' \langle R^{- 2} \rangle} \right]_{\psi}
\right] \right\} $](img1424.png)
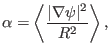
![$\displaystyle A = - (2 \pi)^4 \beta \left\{ \beta_{\psi} - \beta \frac{1}{V' D} [(V'
\alpha)_{\psi} + q (2 \pi)^4 \beta_{\psi}] \right\} $](img1427.png)
![$\displaystyle \Longrightarrow \frac{D}{- (2 \pi)^4 \beta} A = D \beta_{\psi} - \beta \frac{1}{V'} [(V' \alpha)_{\psi} + q (2 \pi)^4 \beta_{\psi}]$](img1428.png)
![$\displaystyle \Longrightarrow \frac{D}{- \beta (2 \pi)^4} A = D \beta_{\psi} - \beta \frac{1}{V'} [V'' \alpha + V' \alpha_{\psi} + q (2 \pi)^4 \beta_{\psi}]$](img1429.png)
![$\displaystyle \left. \Longrightarrow \frac{D}{- \beta (2 \pi)^4} A = \alpha \be...
...c{1}{V'} V' \alpha_{\psi} - \beta \frac{1}{V'} q (2 \pi)^4 \beta_{\psi} \right]$](img1431.png)
![$\displaystyle \left. \Longrightarrow \frac{D}{- \beta (2 \pi)^4} A = \alpha \be...
...pha - \beta \alpha_{\psi} - \beta \frac{1}{V'} q (2 \pi)^4 \beta_{\psi} \right]$](img1432.png)
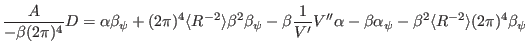
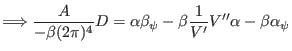
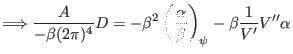
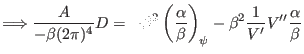
![$\displaystyle \Longrightarrow \frac{A}{- \beta (2 \pi)^4} D = - \beta^2 \left[ ...
...c{\alpha}{\beta} \right)_{\psi} + \frac{1}{V'} V'' \frac{\alpha}{\beta} \right]$](img1437.png)
![$\displaystyle \Longrightarrow \frac{A}{- \beta (2 \pi)^4} D = - \beta^2 \frac{1...
...left( \frac{\alpha}{\beta} \right)_{\psi} V' + V'' \frac{\alpha}{\beta} \right]$](img1438.png)
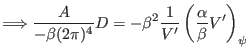
![$\displaystyle \Longrightarrow A = \frac{(2 \pi)^4}{D} \left( \frac{q}{V' \langl...
...^2} \right\rangle \frac{\langle R^{- 2} \rangle}{q} V^{\prime 2} \right]_{\psi}$](img1440.png)