Toroidal current density

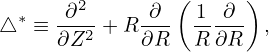
Ampere’s law (49) indicates the toroidal current density J_ϕ is given by

μ0Jϕ = ∂BR − ∂BZ- ∂Z ∂R ( ) = − 1-∂2Ψ-− -∂- 1-∂Ψ- . (52) R ∂Z2 ∂R R ∂R

Deﬁne a diﬀerential operator △^⋆ by

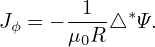∗ ∂2 ∂ ( 1 ∂ ) △ ≡ ∂Z2-+ R∂R- R-∂R- ,

(53)

which is the Laplace operator in cylindrical coordinates for the axisymmertic case, then Eq. (52) is written

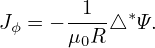1 Jϕ = − ---△ ∗Ψ. μ0R

(54)