Miller’s formula for shaped ﬂux surfaces

16.6 Miller’s formula for shaped ﬂux surfaces

According to Refs. [8, 20], Miller’s formula for a series of shaped ﬂux surfaces is given by

R = R0(r)+ rcos{𝜃+ arcsin[δ(r)sin𝜃]},

(496)

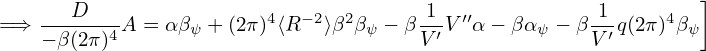Z = κ(r)rsin 𝜃,

(497)

where κ(r) and δ(r) are elongation and triangularity proﬁle, R₀(r) is the Shafranov shift proﬁle, which is given by

aR′[ (r)2] R0(r) = R0 (a)− --0-1 − -- , 2 a

(498)

where R₀′ is a constant, R₀(a) is the major radius of the center of the boundary ﬂux surface. The triangularity proﬁle is

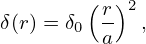(r)2 δ(r) = δ0-- , a

(499)

and the elongation proﬁle is

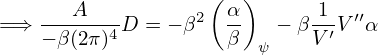(r)4 κ(r) = κ0 − 0.3+ 0.3 a .

(500)

The nominal ITER parameters are κ₀ = 1.8, δ₀ = 0.5 and R₀′ = −0.16. I wrote a code to plot the shapes of the ﬂux surface (/home/yj/project/miller_ﬂux_surface). An example of the results is given in Fig. 35.

Fig. 35: Flux-surfaces given by Eqs. (496) and (497) with r∕a varying from 0.1 to 1.0 (corresponding boundary surface). Other parameters are R₀(a)∕a = 3, κ₀ = 1.8, δ₀ = 0.5, R₀′ = −0.16.

[next] [prev] [prev-tail] [front] [up]