16.8 Ballooning transformation

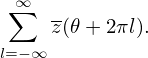
To construct a periodic function about 𝜃, we introduces a function z(𝜃) which is defined over −∞ < 𝜃 < ∞ and vanishes sufficiently fast as |𝜃|→∞ so that the following infinite summation converge:

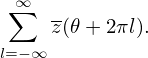(502)

If we use the above sum to define a function

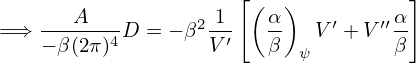(503)

then it is obvious that

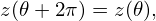(504)

i.e., z(𝜃) is a periodic function about 𝜃 with period of 2π.

If we use the right-hand-side of Eq. (503) to represent z(𝜃), then we do not need to worry about the periodic property of z(𝜃) (the periodic property is guaranteed by the representation)