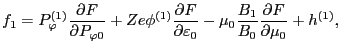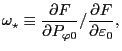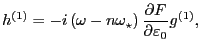Write 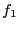 as
as
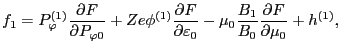 |
(113) |
and substitute this into Eq. (112), giving an equation of 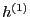 ,
,
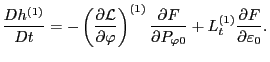 |
(114) |
Eq. (114) agrees with Eq. (35) in Porcelli's
paper[1]. For notation convenience, we define
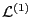 as
as
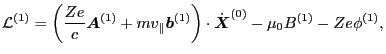 |
(115) |
which can be called ``perturbed Lagrangian'' (I do not care the name of
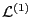 , and
, and
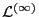 is only a notation without any
physical meaning since I do not need this meaning to derive anything). Since
we are considering toroidal symmetrical case, different toroidal harmonics of
perturbation are independent. Thus we can consider a single toroidal harmonic,
i.e, the
is only a notation without any
physical meaning since I do not need this meaning to derive anything). Since
we are considering toroidal symmetrical case, different toroidal harmonics of
perturbation are independent. Thus we can consider a single toroidal harmonic,
i.e, the 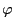 dependence of components of
dependence of components of
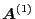 and
and
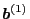 is
is
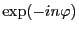 . Further due to that the
equilibrium is time-independent, we can consider a single time harmonic, i.e.,
the time dependence of the perturbation is
. Further due to that the
equilibrium is time-independent, we can consider a single time harmonic, i.e.,
the time dependence of the perturbation is
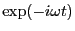 . Then, using
Eq. (115), Eq. (99) is written as
. Then, using
Eq. (115), Eq. (99) is written as
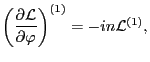 |
(116) |
and
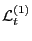 in Eq. (98) is written as
in Eq. (98) is written as
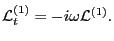 |
(117) |
Using Eqs. (116) and (117), Eq. (114) is written as
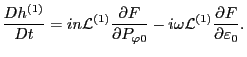 |
(118) |
Define
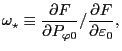 |
(119) |
then Eq. (118) is written as
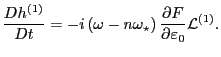 |
(120) |
Eq. (120) agrees with Eq. (40) in Porcelli's paper. Define 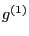 as
as
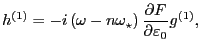 |
(121) |
then 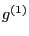 satisfies (note that
satisfies (note that
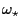 and
and
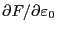 are both functions of constants of motion, thus can be
taken out of the orbit integration)
are both functions of constants of motion, thus can be
taken out of the orbit integration)
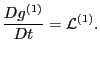 |
(122) |
YouJun Hu
2014-05-19
![]() as
as