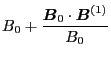The expression
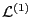 in Eq. (115) can be further
simplified, by noticing that the term
in Eq. (115) can be further
simplified, by noticing that the term
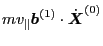 is of the order
is of the order
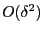 thus can be
neglected, giving
thus can be
neglected, giving
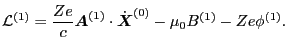 |
(123) |
Next, we provide the proof that the term
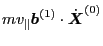 is on the order
is on the order
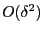 . The
unperturbed velocity of guiding center is given by
. The
unperturbed velocity of guiding center is given by
where
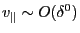 ,
,
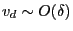 . Next, we
derive the expression of
. Next, we
derive the expression of
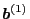 . Using
. Using
we obtain
Therefore
Using this, the term
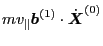 is written as
is written as
where the first two terms on the right-hand side of Eq. (127), which
are on the order
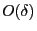 , happen to cancel each other. Since
, happen to cancel each other. Since
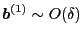 and
and
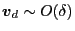 , the
product of these two terms are on the order
, the
product of these two terms are on the order
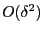 . Therefore Eq.
(134) indicates that the term
. Therefore Eq.
(134) indicates that the term
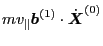 is on the order
is on the order
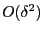 .
.
Next we show that, in the linear approximation, the perturbation in the
strength of the magnetic field, 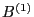 , is equal to
, is equal to
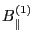 ,
where
,
where
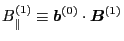 . The total magnetic field can be written as
. The total magnetic field can be written as
Expanding the right-hand side of the above equation at 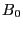 , we obtain
, we obtain
Neglecting the second order term, the above equation is written as
Thus we obtain
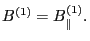 |
(132) |
Eq. (132) seems strange at first glance (actually I think it is wrong
at first glance, Dr. Fu let me know it is right and how to prove it (as given
in the above)). Using Eq. (132), the Lagrangian in Eq. (123)
is written as
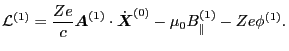 |
(133) |
YouJun Hu
2014-05-19
![]() in Eq. (115) can be further
simplified, by noticing that the term
in Eq. (115) can be further
simplified, by noticing that the term
![]() is of the order
is of the order
![]() thus can be
neglected, giving
thus can be
neglected, giving
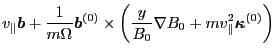
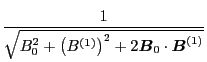
![$\displaystyle \frac{1}{B_0} - \frac{1}{2 B_0^3} \left[ \left( B^{(1)}
\right)^2 + 2 \ensuremath{\boldsymbol{B}}_0 \cdot \ensuremath{\boldsymbol{B}}^{(1)} \right]$](img270.png)
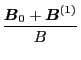
![$\displaystyle \left( \ensuremath{\boldsymbol{B}}_0 + \ensuremath{\boldsymbol{B}...
...math{\boldsymbol{B}}_0 \cdot \ensuremath{\boldsymbol{B}}^{(1)} \right] \right\}$](img273.png)
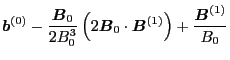
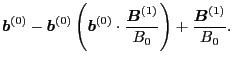
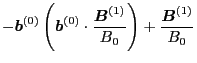
![]() , is equal to
, is equal to
![]() ,
where
,
where
![]() . The total magnetic field can be written as
. The total magnetic field can be written as
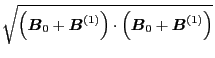
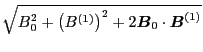
![$\displaystyle \sqrt{B_0^2} + \frac{1}{2 \sqrt{B_0^2}} \left[ \left( B^{(1)}
\ri...
...math{\boldsymbol{B}}_0 \cdot \ensuremath{\boldsymbol{B}}^{(1)} \right] + \ldots$](img292.png)