For the ease of notation, in the following we drop the zero superscript on the
unperturbed orbit. And to distinguish instantaneous and the initial value of
orbit, we add a prime to
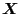 and
and
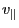 to denote the
instantaneous value. Integrating along the unperturbed orbit, Eq.
(122) is written as
to denote the
instantaneous value. Integrating along the unperturbed orbit, Eq.
(122) is written as
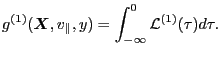 |
(134) |
with the boundary condition
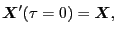 |
(135) |
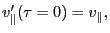 |
(136) |
and the value of the conserved magnetic moment is determined by
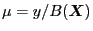 . Using the expression of
. Using the expression of
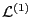 in Eq.
(123), Eq. (134) is written as
in Eq.
(123), Eq. (134) is written as
![$\displaystyle B^{(1)} (\psi, \theta, \varphi, t) = \hat{B}^{(1)} (\psi, \theta) \exp \left[ - i \left( \omega t + n \varphi \right) \right]$](img304.png) |
(137) |
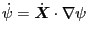 |
(138) |
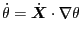 |
(139) |
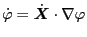 |
(140) |
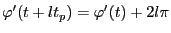 |
(141) |
YouJun Hu
2014-05-19
![]() and
and
![]() to denote the
instantaneous value. Integrating along the unperturbed orbit, Eq.
(122) is written as
to denote the
instantaneous value. Integrating along the unperturbed orbit, Eq.
(122) is written as
![$\displaystyle \int_{- \infty}^0 \left[ \frac{Z e}{c} \ensuremath{\boldsymbol{A}...
...h{\boldsymbol{X}}}' - \mu_0 B_{\parallel}^{(1)} - Z e \phi^{(1)}
\right] d \tau$](img303.png)