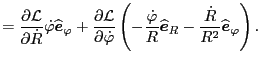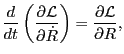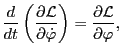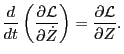Proof of equilavenc between Eq. (8) and
Euler-Lagrange equation (163)
Equation (8) is repeated here, i.e.,
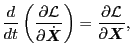 |
(162) |
where
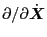 and
and
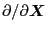 are considered as gradient operators. Note that, in Cartisian
coordinates, the components of Eq. (8) are obviously equivalent to
the respective Euler-Lagrange equations. We now check whether the component
equations in arbitrary coordinate system obtained by evaluating the gradient
of the Lagrangian
are considered as gradient operators. Note that, in Cartisian
coordinates, the components of Eq. (8) are obviously equivalent to
the respective Euler-Lagrange equations. We now check whether the component
equations in arbitrary coordinate system obtained by evaluating the gradient
of the Lagrangian
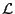 in Eq. (8) are equivalent to the
respective Euler-Lagrange equations in that coordinates system. The
Euler-Lagrange equation in any coordinates is given by
in Eq. (8) are equivalent to the
respective Euler-Lagrange equations in that coordinates system. The
Euler-Lagrange equation in any coordinates is given by
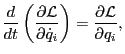 |
(163) |
which is expressed in terms of a single coordinate component, and is
coordinate independent, i..e, it takes the same form for every components of
any coordinate systems.
In this section, I prove that the components of Eq. (8) are
equivalent to the Euler-Lagrange equation (163) in cylindrical
coordinates
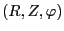 . First, let us consider the term
. First, let us consider the term
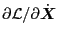 , which, in Cartesian coordinators,
is written as
, which, in Cartesian coordinators,
is written as
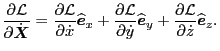 |
(164) |
Using the chain rule, the above equation is written as
Using the transformation relation
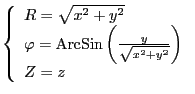 |
(165) |
we obtain
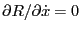 ,
,
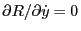 , etc. Thus
, etc. Thus
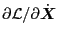 reduces
to
reduces
to
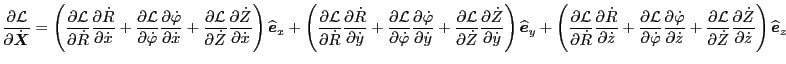 |
(166) |
Using the transformation relation Eq. (165), we obtain
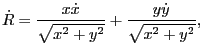 |
(167) |
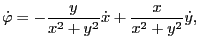 |
(168) |
and
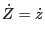 |
(169) |
Noting that
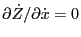 ,
,
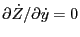 ,
,
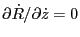 ,
,
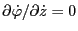 , Eq. (166) is
further written as
, Eq. (166) is
further written as
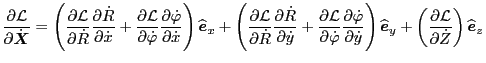 |
(170) |
Using Eqs. (167) and (168), we obtain
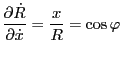 |
(171) |
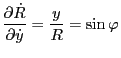 |
(172) |
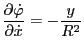 |
(173) |
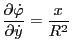 |
(174) |
Using these, Eq. (170) is written as
Using this, the left-hand side of Eq. (8) is written as
Next, consider the right-hand side of Eq. (8), which is the space
gradient of Lagrangian
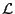 . When I at first considered this problem,
I took it for granted that the space gradient in cylindrical coordinates
should be
. When I at first considered this problem,
I took it for granted that the space gradient in cylindrical coordinates
should be
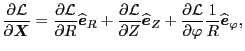 |
(177) |
which turns out to be wrong because this formula does not take into account
that
 depends on
depends on
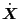 which in turn depends on
the spatial coordinates. The correct way to calculate the space gradient is as
follows:
which in turn depends on
the spatial coordinates. The correct way to calculate the space gradient is as
follows:
It is important to note that
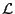 depends on
depends on 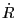 ,
,
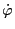 which in turn depend on
which in turn depend on 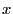 and
and 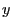 . As a result, there exist
additional terms (the last two terms in both the brackets), which would be
missed if we used the formula in Eq. (177). Equation (178)
is further written as
. As a result, there exist
additional terms (the last two terms in both the brackets), which would be
missed if we used the formula in Eq. (177). Equation (178)
is further written as
Using
Using these results, the last two terms in Eq. (179) is written as
| |
|
![$\displaystyle \left[ - \frac{\partial \mathcal{L}}{\partial \dot{R}} \dot{\varp...
...arphi}{R} \dot{\varphi} \right) \right]
\widehat{\ensuremath{\boldsymbol{e}}}_y$](img421.png) |
|
| |
|
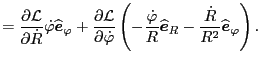 |
(184) |
Using this, Eq. (179) is written as
![$\displaystyle \frac{\partial \mathcal{L}}{\partial \ensuremath{\boldsymbol{X}}}...
...- \frac{\dot{R}}{R^2} \widehat{\ensuremath{\boldsymbol{e}}}_{\varphi} \right] .$](img423.png) |
(185) |
Note that, compared with Eq. (177), the above expression contains
additional terms. The additional terms are the source of confusion when I at
first tried to prove the equivalence between Eqs. (8) and
(163). (I was confused for many days before I fininaly found the
solution given here.) Using Eqs. (185) and (176) in Eq.
(162), we recover the Euler-Lagrange equation in cylindrical
coordinates, i.e.,
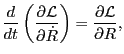 |
(186) |
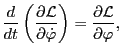 |
(187) |
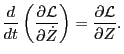 |
(188) |
YouJun Hu
2014-05-19
![]() . First, let us consider the term
. First, let us consider the term
![]() , which, in Cartesian coordinators,
is written as
, which, in Cartesian coordinators,
is written as
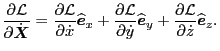
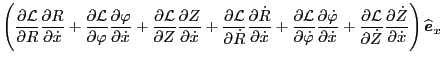
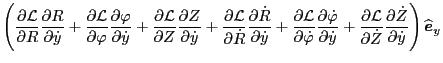
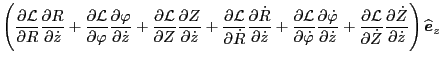
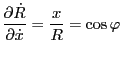
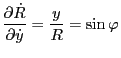
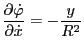
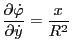
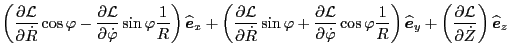
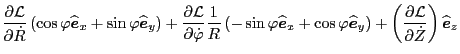
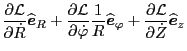
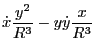
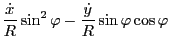
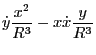
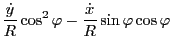
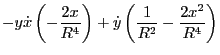
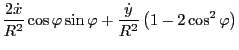
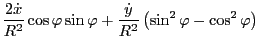
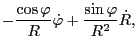
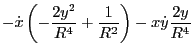
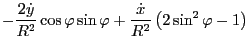
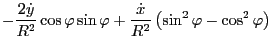
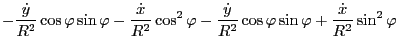
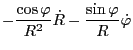
![$\displaystyle \left[ - \frac{\partial \mathcal{L}}{\partial \dot{R}} \dot{\varp...
...arphi}{R} \dot{\varphi} \right) \right]
\widehat{\ensuremath{\boldsymbol{e}}}_y$](img421.png)