For ideal MHD perturbation, the perturbed magnetic field is written as
Using Eq. (142), the vector potential of magnetic perturbation is
written as
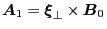 |
(144) |
Using Eq. (143), the parallel component of the magnetic perturbation
is written as
Here I have some important remarks about tensor identities (I had not known
these identities before CaiHuiShan told me). First we note the associate law
applies in this case (Important!), thus
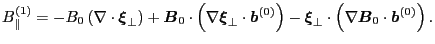 |
(146) |
Second we have the tensor identity (Important!, CaiHuiShan let me know this
identity),
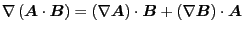 |
(147) |
Using this, the second term of Eq. (146) is written as
where
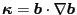 . The last
term of Eq. (146) is written as
. The last
term of Eq. (146) is written as
We note that
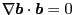 (CaiHuiShan let me
know this), since the tensor identity in Eq. (147) indicates
(CaiHuiShan let me
know this), since the tensor identity in Eq. (147) indicates
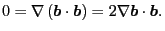 |
(150) |
(It is interesting to note that
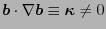 while the above result proves that
while the above result proves that
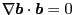 .) Thus Eq. (149) becomes
.) Thus Eq. (149) becomes
Using the above results, the parallel component of the perturbed magnetic
field Eq. (146) becomes
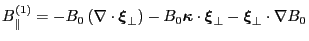 |
(152) |
The perturbed Lagrangian, Eq. (133), is
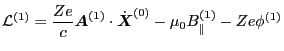 |
(153) |
Using Eq. (144) in Eq. (153) yields
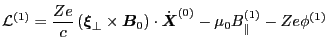 |
(154) |
Using Eq. (78) for
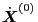 , Eq. (154)
is written as
, Eq. (154)
is written as
Equation (155) agrees with Eq. (55) in Porcelli's
paper[1]. The perturbed electrical field is
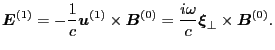 |
(156) |
On the other hand,
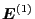 can be expressed as
can be expressed as
Comparing Eqs. (156) and (157), we obtain
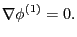 |
(158) |
which indicates the perturbed scalar potential is a constant. We can choose
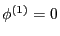 . We consider the case that there is no electrical field in
the equilibrium, i.e.,
. We consider the case that there is no electrical field in
the equilibrium, i.e.,
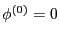 . Using
. Using
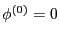 and
and
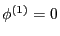 , the Lagrangian in Eq. (155) is written as
, the Lagrangian in Eq. (155) is written as
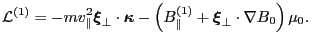 |
(159) |
Substituting the expression of
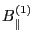 in Eq. (152)
into the above equation, we obtain
in Eq. (152)
into the above equation, we obtain
We note an important fact that magnetic curvature
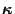 is
perpendicular to
is
perpendicular to
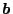 . This is because that
. This is because that
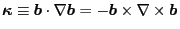 . The last equality is due to the vector identity
. The last equality is due to the vector identity
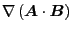 =
=
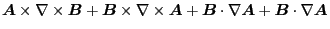 . Using this fact, Eq. (160) can also be written as
. Using this fact, Eq. (160) can also be written as
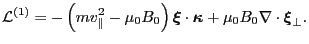 |
(161) |
Eq. (161) agrees with Eq. (58) in Porcelli's
paper[1].
YouJun Hu
2014-05-19